
【题目】(本小题满分12分)某中学欲制定一项新的制度,学生会为此进行了问卷调查,所有参与问卷调查的人中,持有“支持”、“不支持”和“既不支持也不反对”的人数如下表所示:
支持 | 既不支持也不反对 | 不支持 | |
高一学生 | 800 | 450 | 200 |
高二学生 | 100 | 150 | 300 |
(Ⅰ)在所有参与问卷调查的人中,用分层抽样的方法抽取![]() 个人,已知从“支持”的人中抽取了45人,求
个人,已知从“支持”的人中抽取了45人,求![]() 的值;
的值;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人,从这5人中任意选取2人,求至少有1人是高一学生的概率.
【答案】(Ⅰ)100;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)根据支持的总人数及抽取的人数求出抽样比,再依此求出样本容量;
(Ⅱ)持“不支持”态度的共有500人,抽样比为百分之一,确定其中高一、高二的人数,然后根据古典概型号的概率公式求解.
试题解析:解:(1)根据分层抽样的原理,每层抽取的样本的比例是相等的,所以有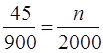 ,解得
,解得![]() ;
;
(2)由题意:高一、高二持“不支持”态度的共有500人,抽样比为百分之一,所以抽取的5人中,有高一学生2人,记为![]() 高二学生3人,记为
高二学生3人,记为![]() ;从这5人中任选2人,有10种不同的结果,它们是:
;从这5人中任选2人,有10种不同的结果,它们是: ![]() .由于是任意选取的,所以每个结果出现的可能性是相等的,记事件A为“至少有一人是高一学生”,则事件A包含
.由于是任意选取的,所以每个结果出现的可能性是相等的,记事件A为“至少有一人是高一学生”,则事件A包含![]() 共7个基本结果,根据古典概型的概率公式,事件A发生的概率
共7个基本结果,根据古典概型的概率公式,事件A发生的概率![]()


科目:高中数学 来源: 题型:
【题目】如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2﹣4y﹣4=0,双曲线的左、右顶
点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为F1、F2 , 试在“8”字形曲线上求点P,使得
∠F1PF2是直角.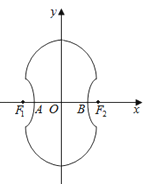
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点P(﹣3![]() , 4),它的渐近线方程为y=±
, 4),它的渐近线方程为y=±![]() x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
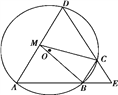
【题目】如图,四边形ABCD是☉O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(Ⅰ)证明:∠D=∠E;
(Ⅱ)设AD不是☉O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆x2+y2+2x﹣4y﹣6=0的圆心和半径分别是( )
A.(﹣1,﹣2),11
B.(﹣1,2),11
C.(﹣1,﹣2), ![]()
D.(﹣1,2), ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com