解:(Ⅰ)当n=1时,有
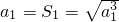
,由于a
n>0,所以a
1=1
当n=2时,有
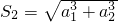
,即
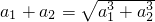
,将a
1=1代入上式,由于a
n>0,所以a
2=2
(Ⅱ)由
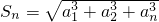
得,a
13+a
23+…+a
n3=(a
1+a
2+…+a
n)
2①
则有a
13+a
23+…+a
n3+a
n+13=(a
1+a
2+…+a
n+a
n+1)
2②
②-①,得a
n+13=(a
1+a
2+…+a
n+a
n+1)
2-(a
1+a
2+…+a
n)
2由于a
n>0,所以a
n+12=2(a
1+a
2+…+a
n)+a
n+1③
同样有a
n2=2(a
1+a
2+…+a
n-1)+a
n④
③-④,得a
n+12-a
n2=a
n+1+a
n,所以a
n+1-a
n=1(n≥2),
由于a
2-a
1=1,即当n≥1时都有a
n+1-a
n=1,
所以数列{a
n}是首项为1,公差为1的等差数列
故a
n=n
分析:(Ⅰ)由
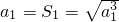
,a
n>0,知a
1=1.
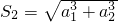
,即
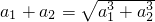
,由此能求出a
2=2.
(Ⅱ)由
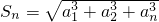
得,a
13+a
23+…+a
n3=(a
1+a
2+…+a
n)
2,故a
13+a
23+…+a
n3+a
n+13=(a
1+a
2+…+a
n+a
n+1)
2,由此得a
n+13=(a
1+a
2+…+a
n+a
n+1)
2-(a
1+a
2+…+a
n)
2,由此能够导出a
n+12-a
n2=a
n+1+a
n,所以a
n+1-a
n=1(n≥2),所以数列{a
n}是首项为1,公差为1的等差数列,由此能求出其通项公式.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意递推公式的合理运用.

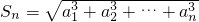 .
.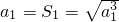 ,由于an>0,所以a1=1
,由于an>0,所以a1=1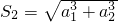 ,即
,即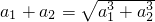 ,将a1=1代入上式,由于an>0,所以a2=2
,将a1=1代入上式,由于an>0,所以a2=2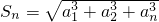 得,a13+a23+…+an3=(a1+a2+…+an)2①
得,a13+a23+…+an3=(a1+a2+…+an)2①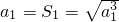 ,an>0,知a1=1.
,an>0,知a1=1.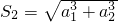 ,即
,即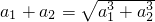 ,由此能求出a2=2.
,由此能求出a2=2.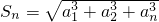 得,a13+a23+…+an3=(a1+a2+…+an)2,故a13+a23+…+an3+an+13=(a1+a2+…+an+an+1)2,由此得an+13=(a1+a2+…+an+an+1)2-(a1+a2+…+an)2,由此能够导出an+12-an2=an+1+an,所以an+1-an=1(n≥2),所以数列{an}是首项为1,公差为1的等差数列,由此能求出其通项公式.
得,a13+a23+…+an3=(a1+a2+…+an)2,故a13+a23+…+an3+an+13=(a1+a2+…+an+an+1)2,由此得an+13=(a1+a2+…+an+an+1)2-(a1+a2+…+an)2,由此能够导出an+12-an2=an+1+an,所以an+1-an=1(n≥2),所以数列{an}是首项为1,公差为1的等差数列,由此能求出其通项公式.
