
【题目】已知函数f(x)=kx,g(x)= ![]() .
.
(1)求函数g(x)= ![]() 的单调区间;
的单调区间;
(2)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围.
【答案】
(1)解:∵g(x)= ![]() ,x>0,故其定义域为(0,+∞),
,x>0,故其定义域为(0,+∞),
∴ ![]() ,
,
令g′(x)>0,得0<x<e,
令g′(x)<0,得x>e,
故函数 ![]() 的单调递增区间为(0,e),单调递减区间为(e,+∞).
的单调递增区间为(0,e),单调递减区间为(e,+∞).
(2)解:∵ ![]() ,∴k
,∴k ![]() ,
,
令 ![]() ,
,
又 ![]() ,
,
令h′(x)=0,解得 ![]() ,
,
当x在(0,+∞)内变化时,h′(x),h(x)变化如下表
x |
|
|
|
h′(x) | + | 0 | ﹣ |
h(x) | ↗ |
| ↘ |
由表知,当时函数h(x)有最大值,且最大值为 ![]() ,
,
所以 ![]() .
.
【解析】(1)由g(x)= ![]() ,知
,知 ![]() ,由此能求出函数
,由此能求出函数 ![]() 的单调区间.(2)由
的单调区间.(2)由 ![]() ,知k
,知k ![]() ,令
,令 ![]()
![]() ,知
,知 ![]() ,由此能求出实数k的取值范围.
,由此能求出实数k的取值范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
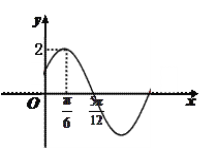
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a∈R,若对任意的非零的实数x1 , 存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最小值为( )
,其中a∈R,若对任意的非零的实数x1 , 存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最小值为( )
A.![]()
B.5
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c.已知 ![]() =
= ![]() .
.
(1)求角A的大小;
(2)当a=6时,求△ABC面积的最大值,并指出面积最大时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中秋节即将到来,为了做好中秋节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片![]() 剪去四个全等的等腰三角形
剪去四个全等的等腰三角形![]() ,
, ![]() ,
, ![]() ,
, ![]() 再将剩下的阴影部分折成一个四棱锥形状的包装盒
再将剩下的阴影部分折成一个四棱锥形状的包装盒![]() ,其中
,其中![]() 重合于点
重合于点![]() ,
, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合(如图所示).
重合(如图所示).
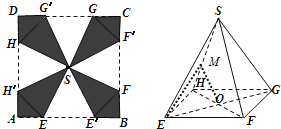
(1)求证:平面![]() 平面
平面![]() ;
;
(2)已知![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)判断并证明函数f(x)的奇偶性
(2)判断并证明当x∈(﹣1,1)时函数f(x)的单调性;
(3)在(2)成立的条件下,解不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( ) 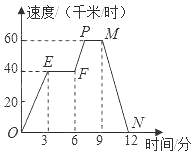
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com