
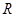 的函数:
的函数: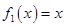 ,
,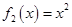 ,
,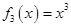 ,
,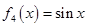 ,
,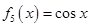 ,
,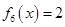 .
.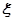 的分布列和数学期望.
的分布列和数学期望.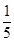 ;(2)详见解析.
;(2)详见解析.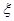 的全部可能取值,利用条件概率的计算公式计算随机变量子在相应的取值下对应的概率,从而列举出随机变量的分布列,最终计算出随机变量的数学期望.
的全部可能取值,利用条件概率的计算公式计算随机变量子在相应的取值下对应的概率,从而列举出随机变量的分布列,最终计算出随机变量的数学期望.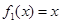 ,
,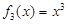 ,
,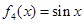 ,
,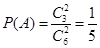 ;
;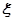 可取1,2,3,4 ,
可取1,2,3,4 , ,
, 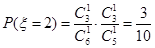
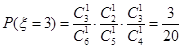 ,
, 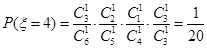 ,
, 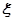 的分布列为
的分布列为 | 1 | 2 | 3 | 4 |
 | 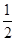 | 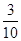 | 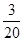 | 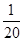 |
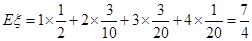
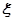 的数学期望为
的数学期望为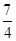 .
.

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
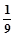 (已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(已知甲回答每个问题的正确率相同,并且相互之间没有影响)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.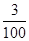 | B.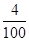 | C.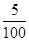 | D.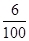 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com