
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上任意一点,以
上任意一点,以![]() 为直径作圆
为直径作圆![]() .
.
(1)判断圆![]() 与坐标
与坐标![]() 轴的位置关系,并证明你的结论;
轴的位置关系,并证明你的结论;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() ,且
,且![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“p且![]() ”为假命题,则p、q均为假命题;②命题“若a>b,则
”为假命题,则p、q均为假命题;②命题“若a>b,则![]() ”的否命题为“若a≤b,则
”的否命题为“若a≤b,则![]() ”;③“x∈R,
”;③“x∈R,![]() 的否定是“
的否定是“![]() ”;④在△ABC中,“A>B”是“
”;④在△ABC中,“A>B”是“![]() ”的充要条件;其中正确的命题的个数是( )
”的充要条件;其中正确的命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点,且交椭圆于A,B两点,线段AB的中点是
的右焦点,且交椭圆于A,B两点,线段AB的中点是![]() ,
,
(1)求椭圆的方程;
(2)过原点的直线l与线段AB相交(不含端点)且交椭圆于C,D两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ’(
’(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 为抛物线
为抛物线![]() 的对称轴与其准线的交点,过
的对称轴与其准线的交点,过![]() 作抛物线
作抛物线![]() 的切线,切点为
的切线,切点为![]() ,若点
,若点![]() 恰好在以
恰好在以![]() ,
,![]() 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数![]() 浓度,制定了空气质量标准:
浓度,制定了空气质量标准:
空气污染质量 |
|
|
|
|
|
|
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
某市政府为了打造美丽城市,节能减排,从2010年开始考查了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号为字母的,前13个视为单号,后13个视为双号).
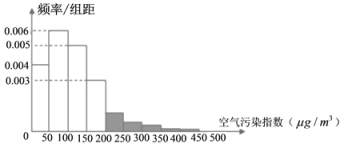
(1)某人计划11月份开车出行,求因空气污染被限号出行的概率;
(2)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行三年来的11月份共90天的空气质量进行统计,其结果如表:
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 16 | 39 | 18 | 10 | 5 | 2 |
根据限行前六年180天与限行后90天的数据,计算并填写![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为空气质量的优良与汽车尾气的排放有关.
的把握认为空气质量的优良与汽车尾气的排放有关.
空气质量优良 | 空气质量污染 | 合计 | |
限行前 | |||
限行后 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 其中
其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的极值;
的极值;
(3)设![]() (
(![]() 表示p,q中的最小值),若
表示p,q中的最小值),若![]() 在
在![]() 上恰有三个零点,求实数k的取值范围.
上恰有三个零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com