
【题目】已知f(x)=3x2﹣2x,数列{an}的前n项和为Sn , 点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
【答案】
(1)解:∵f(x)=3x2﹣2x,数列{an}的前n项和为Sn,
点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴ ![]() ,
,
当n≥2时,an=Sn﹣Sn﹣1=(3n2﹣2n)﹣[3(n﹣1)2﹣2(n﹣1)]=6n﹣5,
当n=1时,a1=S1=3﹣2=1,满足上式,
∴an=6n﹣5,n∈N*.的
(2)解:由(1)得 ![]() =
= ![]() =
= ![]() ,
,
∴Tn= ![]()
= ![]() ,
,
∴使得Tn< ![]() 对所有n∈N*都成立的最小正整数m必须且仅须满足
对所有n∈N*都成立的最小正整数m必须且仅须满足 ![]() ,
,
即m≥10,∴满足要求的最小整数m=10.
【解析】1、利用点在直线上可得到S n = 3 n2 2 n,根据an和 Sn关系式求出 an=6n﹣5。
2、根据(1)的结论可得出数列{bn}的通项公式,求出 Tn 的式子用列项相消法得到 ![]()
![]() ,再由放缩法得到这个式子小于
,再由放缩法得到这个式子小于![]() ,由已知可求得
,由已知可求得 ![]() ≤
≤ ![]() ,故得结果。
,故得结果。
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系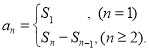 即可以解答此题.
即可以解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】已知直线 ![]() ,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
(Ⅰ)求实数m的取值范围;
(Ⅱ)当m=﹣2时,试判断直线l与该圆的位置关系,若相交,求出相应弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx﹣cosx)2+ ![]() sin(2x+
sin(2x+ ![]() )(x∈R).
)(x∈R).
(1)求函数f(x)的递减区间;
(2)若f(α)= ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求cos(2α+
),求cos(2α+ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 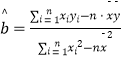 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(
的前 n 项和为 Sn ,且(3-m)Sn+2man=m+3(![]() ) ,其中 m 为常数,且
) ,其中 m 为常数,且 ![]() .
.
①求证: ![]() 是等比数列;
是等比数列;
②若数列 ![]() 的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,
的公比为q=f(m) ,数列 {bn} 满足 b1=a1 ,![]() ,求证:
,求证: ![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF.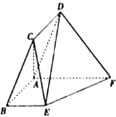
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义 ![]() 为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为
为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为 ![]() ,又bn=
,又bn= ![]() ,则
,则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以 ![]() 为概率的事件是( )
为概率的事件是( )
A.都不是一等品
B.恰有一件一等品
C.至少有一件一等品
D.至多一件一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com