
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 时,满足
时,满足![]() .
.
(1)求证:![]() ;
;
(2)求证:数列![]() 为等差数列;
为等差数列;
(3)若![]() ,公差
,公差![]() ,问是否存在
,问是否存在![]() ,
,![]() ,使得
,使得![]() ?如果存在,求出所有满足条件的
?如果存在,求出所有满足条件的![]() ,
,![]() ,如果不在,请说明理由.
,如果不在,请说明理由.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.对于
数列.对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两项
中任取两项![]() ,
,![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
,![]() ,这样得到一个
,这样得到一个![]() 项的新数列
项的新数列![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() ,得到的新数列记作
,得到的新数列记作![]() ,
,![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(1)设![]() ,
,![]() ,
,![]() 请写出
请写出![]() 的所有可能的结果;
的所有可能的结果;
(2)求证:对于一个![]() 项的
项的![]() 数列
数列![]() 操作
操作![]() 总可以进行
总可以进行![]() 次;
次;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 求
求![]() 的可能结果,并说明理由.
的可能结果,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
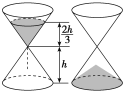
【题目】中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器,如图,某沙漏由上、下两个圆锥容器组成,圆锥的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
A.2 cmB.![]() cmC.
cmC.![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过右焦点![]() 作一条不与坐标轴平行的直线
作一条不与坐标轴平行的直线![]() ,若
,若![]() 交椭圆
交椭圆![]() 与
与![]() 、
、![]() 两点,点
两点,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
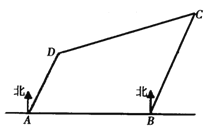
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() ;
;
②若集合![]() 中只有一个元素,则
中只有一个元素,则![]() ;
;
③函数![]() 在
在![]() 上是增函数;
上是增函数;
④方程![]() 的实根的个数是1.
的实根的个数是1.
所有正确命题的序号是______(请将所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 、
、![]() 的定义域均为
的定义域均为![]() ,若对任意
,若对任意![]() ,且
,且![]() ,具有
,具有![]() ,则称函数
,则称函数![]() 为
为![]() 上的单调非减函数,给出以下命题:① 若
上的单调非减函数,给出以下命题:① 若![]() 关于点
关于点![]() 和直线
和直线![]() (
(![]() )对称,则
)对称,则![]() 为周期函数,且
为周期函数,且![]() 是
是![]() 的一个周期;② 若
的一个周期;② 若![]() 是周期函数,且关于直线
是周期函数,且关于直线![]() 对称,则
对称,则![]() 必关于无穷多条直线对称;③ 若
必关于无穷多条直线对称;③ 若![]() 是单调非减函数,且关于无穷多个点中心对称,则
是单调非减函数,且关于无穷多个点中心对称,则![]() 的图象是一条直线;④ 若
的图象是一条直线;④ 若![]() 是单调非减函数,且关于无穷多条平行于
是单调非减函数,且关于无穷多条平行于![]() 轴的直线对称,则
轴的直线对称,则![]() 是常值函数;以上命题中,所有真命题的序号是_________
是常值函数;以上命题中,所有真命题的序号是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 的边长为
的边长为![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若![]() ,分别是椭圆长轴的左,右端点,动点
,分别是椭圆长轴的左,右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() ,的定点
,的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com