
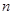 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是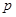 .
. 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数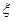 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求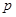 和
和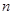 .
.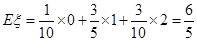 ;(2)
;(2)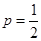 ,
,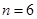 .
. ,所以5个球中有2个白球
,所以5个球中有2个白球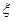 可取0,1,2.························· 1分
可取0,1,2.························· 1分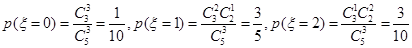 .······· 4分
.······· 4分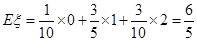 .······················· 6分
.······················· 6分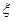 服从参数为
服从参数为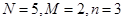 的超几何分布,则
的超几何分布,则 ……………………6分
……………………6分 ,···················· 8分
,···················· 8分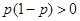 所以不等式可化为
所以不等式可化为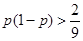 ,
,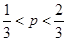 ,即
,即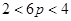 .·················· 10分
.·················· 10分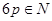 ,所以
,所以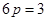 ,即
,即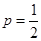 ,
,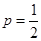 ,所以
,所以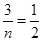 ,所以
,所以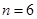 .···················· 12分
.···················· 12分

科目:高中数学 来源:不详 题型:解答题
 和
和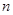 ,将
,将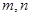 作为Q点的横、纵坐标,
作为Q点的横、纵坐标, 的夹角为
的夹角为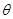 ,求
,求 的概率;
的概率; 内的概率.
内的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 ;不成功的概率依次为
;不成功的概率依次为 、
、 .
. ,求
,求 的分布列,并计算
的分布列,并计算 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 排队人数 |  |  |  |  |  |  人以上 人以上 |
| 概率 |  |  |  |  |  |  |
 人排队的概率是多少?
人排队的概率是多少?  人排队的概率是多少
人排队的概率是多少查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com