
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对4个命题分别进行判断,即可得出结论.
解答 解:①∵f(x)=x3-3x2,∴f′(x)=3x2-6x,
由f′(x)=0,得x=0或x=2,
当x∈(-∞,0)时,f′(x)>0;当x∈(0,2)时,f′(x)<0;当x∈(2,+∞)时,f′(x)>0.
∴f(x)的增区间是(-∞,0),(2,+∞);减区间是(0,2).
∴f(x)极大值=f(0)=0,f(x)极小值=f(2)=-4.
∴①不正确;
由①可得f(x)=x3-3x2在(-∞,2)上有最大值0,不正确;
③复数z=a+b i(a,b∈R)为纯虚数的充要条件是实部为0且虚部不为0.a=0时,复数z=a+b i(a,b∈R)不一定为纯虚数.若复数z=a+b i(a,b∈R)为纯虚数,必有a=0.所以a=0是复数z=a+b i(a,b∈R)为纯虚数的必要但不充分条件;若函数y=f(x)在点x=x0处有极值,则f′(x0)=0;反之不一定,例如取f(x)=x3,虽然f′(0)=0,但是函数f(x)在x=0处没有极值.因此f′(x0)=0是可导函数y=f(x)在点x=x0处有极值的必要非充分条件.∴¬p∧q为真,正确.
④若z1,z2∈C,且z12+z22=0,则z1=z2=0;z1=i,z2=-i,时满足题意,显然不正确.
故选:A.
点评 本题考查命题的真假判断,考查导数知识的运用,考查复数知识,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 到x轴距离为5的点的轨迹是y=5 | |
| B. | 方程$\frac{x}{y}=1$表示的曲线是直角坐标平面上第一象限的角平分线 | |
| C. | 方程(x-y)2+(xy-1)2=0表示的曲线是一条直线和一条双曲线 | |
| D. | 2x2-3y2-2x+m=0通过原点的充要条件是m=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
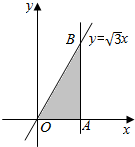 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
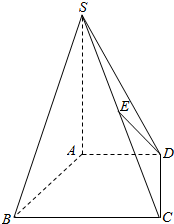 如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.
如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com