
【题目】已知F是抛物线x2=4y的焦点,P是抛物线上的一个动点,且A的坐标为(0,﹣1),则 ![]() 的最小值等于 .
的最小值等于 .
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是 . ①
)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是 . ① ![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
② ![]() f(
f( ![]() )<f(
)<f( ![]() )
)
③f(0)>2f( ![]() )
)
④f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)(理)求ξ的分布列和数学期望 (文)求P(ξ=1)的值
(3)(理)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,宜城各医院产科就已经是一片忙碌,至今热度不减.卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中20个是“二孩”宝宝;市妇幼保健院共有30个猴宝宝降生,其中10个是“二孩”宝宝. (I)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询.
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(Ⅱ)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
附: ![]()
P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
k0 | 0.708 | 1.323 | 2.072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 表示两条不同的直线,
表示两条不同的直线, ![]() 表示一个平面,给出下列四个命题:
表示一个平面,给出下列四个命题:
① ![]() ;②
;② ![]() ;
;
③ ![]() ;④
;④ ![]() .
.
其中正确命题的序号是( )
A.①②
B.②③
C.②④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥 ![]() 中,底面
中,底面 ![]() 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ![]() 底面
底面 ![]() ,且
,且 ![]() ,
, ![]() 是侧棱
是侧棱 ![]() 上的动点.
上的动点.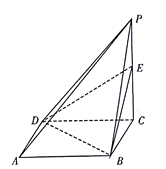
(1)求四棱锥 ![]() 的表面积;
的表面积;
(2)是否在棱 ![]() 上存在一点
上存在一点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ;若存在,指出点
;若存在,指出点 ![]() 的位置,并证明;若不存在,请说明理由.
的位置,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合.曲线 ![]() (t为参数),曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ. (Ⅰ)将曲线C1 , C2分别化为普通方程、直角坐标方程,并说明表示什么曲线;
(t为参数),曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ. (Ⅰ)将曲线C1 , C2分别化为普通方程、直角坐标方程,并说明表示什么曲线;
(Ⅱ)设F(1,0),曲线C1与曲线C2相交于不同的两点A,B,求|AF|+|BF|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com