以下有四种说法:
(1)若p∨q为真,p∧q为假,则p与q必为一真一假;
(2)若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则an=2n,n∈N*;
(3)若f′(x0)=0,则f(x)在x=x0处取得极值;
(4)若定义在R上的函数f(x)满足f(x+2)=-f(x-1),则6为函数f(x)的周期.
以上四种说法,其中正确说法的序号为________.
解:对于(1),∵p∨q为真,p∧q为假,
∴p与q必为一真一假,故(1)正确;
(2)中,∵数列{an}的前n项和Sn=n2+n+1中的常数项不为0,
∴数列{an}不是等差数列,
∴an=2n,n∈N*是错误的,应为分段函数(当n=1时,a1=3;当n≥2时,an=2n,n∈N*);
对于(3),不妨令y=x3,y′=3x2,当x=0时,f′(0)=0,但x=0不是零点,f(x)在x=0处不取得极值,故(3)错误;
对于(4),令t=x-1,则f(t+3)=-f(t),
∴f[(t+3)+3]=-f(t+3)=f(t),
即f(t+6)=f(t),从而f(x+6)=f(x),
∴6为函数f(x)的周期,故(4)正确.
综上所述,(1)(4)正确.
故答案为:(1)(4).
分析:(1)由命题真假判断的真值表即可判断①的正误;
(2)由数列{an}的前n项和Sn=n2+n+1中的常数项不为0,可知数列{an}不是等差数列,从而可判断其正误;
(3)可举例y=x3,当x=0时,f′(0)=0,f(x)在x=0处不取得极值;
(4)可令t=x-1,证得f(t+3)=-f(t),从而可判断(4)正确.
点评:本题考查命题的真假判断与应用,考查函数的周期的判断,考查数列与导数,掌握各部分的基础知识是综合应用的关键,属于中档题.



 口算题天天练系列答案
口算题天天练系列答案

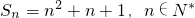 ,则
,则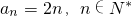 ;
;