
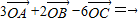 且AB:BC:CA=5:4:3,下列结论错误的是( )
且AB:BC:CA=5:4:3,下列结论错误的是( )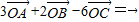 变形,可变为
变形,可变为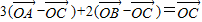 即
即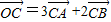 ,再由AB:BC:CA=5:4:3,不妨令AB,BC,CA长度分别为5,4,3,由勾股定理可得出此三角形是直角三角形,由这些几何特征作出如图的图形,由图对四个选项逐一判断找出错误选项,A选项由图就可判断出正确,B选项可先根据图形求出三个三角形的面积,作比验证;C选项可求出O到AB,BC,CA的距离,再求它们的比验证,D选项由图即可观察出正误
,再由AB:BC:CA=5:4:3,不妨令AB,BC,CA长度分别为5,4,3,由勾股定理可得出此三角形是直角三角形,由这些几何特征作出如图的图形,由图对四个选项逐一判断找出错误选项,A选项由图就可判断出正确,B选项可先根据图形求出三个三角形的面积,作比验证;C选项可求出O到AB,BC,CA的距离,再求它们的比验证,D选项由图即可观察出正误 解:由题意,已知点O是△ABC所在平面内的一点,
解:由题意,已知点O是△ABC所在平面内的一点,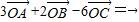 可变为
可变为 即
即

 ×4×9=18,S△COA=
×4×9=18,S△COA= ×3×8=12,S△AOB=S△BOC+S△COA+S△CB=18+12+6=36,
×3×8=12,S△AOB=S△BOC+S△COA+S△CB=18+12+6=36, =
= ,于是点O到AB,BC,CA距离的比是
,于是点O到AB,BC,CA距离的比是 :9:8=72:45:40,故C选项中的结论正确
:9:8=72:45:40,故C选项中的结论正确 与AB:BC:CA=5:4:3,解答本题也要注意赋值的技巧,由于本题中两个选项研究位置关系,两个选项研究的是比值关系,故采取了特值法不妨令AB,BC,CA长度分别为5,4,3,此做法大大降低了计算难度,做题时要恰当使用,本题考查了数形结合的思想,判断推理的能力,综合性较强,难度较大
与AB:BC:CA=5:4:3,解答本题也要注意赋值的技巧,由于本题中两个选项研究位置关系,两个选项研究的是比值关系,故采取了特值法不妨令AB,BC,CA长度分别为5,4,3,此做法大大降低了计算难度,做题时要恰当使用,本题考查了数形结合的思想,判断推理的能力,综合性较强,难度较大 

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
 (2012•九江一模)已知点G是△ABC的外心,
(2012•九江一模)已知点G是△ABC的外心,| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| GA |
| AB |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点G是△ABC的外心,![]() 是三个单位向量,且满足2
是三个单位向量,且满足2![]() ,|
,|![]() |=|
|=|![]() |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|![]() |的最大值为 .
|的最大值为 .

查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌十九中高三(上)第四次月考数学试卷(理科)(解析版) 题型:填空题
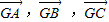 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,|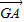 |=|
|=|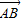 |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .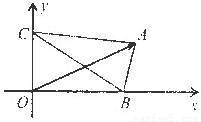
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(文科)(解析版) 题型:解答题
 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,|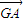 |=|
|=|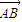 |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .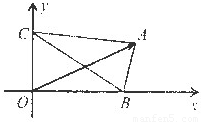
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(理科)(解析版) 题型:解答题
 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,|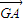 |=|
|=| |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .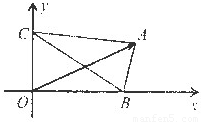
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com