
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
【答案】①②④
【解析】
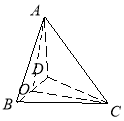
![]() 试题分析:取BD的中点为O连接AO、CO,则AO⊥BD、CO⊥BD,可得BD⊥面ACO,从而有AC⊥BD, ①正确;设正方形ABCD的边长为2,由①知
试题分析:取BD的中点为O连接AO、CO,则AO⊥BD、CO⊥BD,可得BD⊥面ACO,从而有AC⊥BD, ①正确;设正方形ABCD的边长为2,由①知![]() ,所以②正确;因为平面ABD与平面BCD垂直,又AO⊥BD,所以AO⊥平面BCD,所以∠ABO即为AB 与平面BCD所成的角,由△BAD为等腰直角三角形可知,∠ABO=45°,③不正确;取AD的中点为E,AC的中点为F,连接OE、OF、EF,则有OE∥AB、EF∥CD,所以AB与CD所成角即∠OEF,且
,所以②正确;因为平面ABD与平面BCD垂直,又AO⊥BD,所以AO⊥平面BCD,所以∠ABO即为AB 与平面BCD所成的角,由△BAD为等腰直角三角形可知,∠ABO=45°,③不正确;取AD的中点为E,AC的中点为F,连接OE、OF、EF,则有OE∥AB、EF∥CD,所以AB与CD所成角即∠OEF,且![]() ,又OF为Rt△AOC斜边上的中线,所以
,又OF为Rt△AOC斜边上的中线,所以![]() ,因此∠OEF=60°,也就是AB与CD所成的角是60°, ④正确.
,因此∠OEF=60°,也就是AB与CD所成的角是60°, ④正确.


科目:高中数学 来源: 题型:
【题目】已知直线l过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于![]() .
.
(1)求直线l的方程.
(2)求圆心在直线l上且经过点M(2,1),N(4,-1)的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
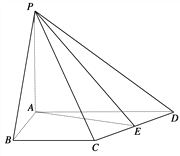
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com