
月份 | 1 | 2 | 3 | 4 |
用电量 | 4.5 | 4 | 3 | 2.5 |
 与月份
与月份 间有较好的线性相关关系,其线性回归直线方程是
间有较好的线性相关关系,其线性回归直线方程是 ,则
,则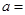 ( )
( ) 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 的男生有30人,女生4人;身高<170的男生有10人。
的男生有30人,女生4人;身高<170的男生有10人。 列联表:
列联表:


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 男 | 女 | 总计 |
| 爱好 | 40 | | |
| 不爱好 | | 30 | |
| 总计 | | | |
 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A. x;和y正相关 |
| B. x和y的相关系数为直线l的斜率 |
| C. x和y的相关系数在-1到0之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 认为作业多 | 认为作业不多 | 总数 |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
 .
. | 0.050 | 0.025 | 0.010 | 0.001 |
 | 3.841 | 5.024 | 6.635 | 10.828 |
 的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”; 的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”; 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”; 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.身高一定是145.83 cm | B.身高在145.83 cm以上 |
| C.身高在145.83 cm左右 | D.身高在145.83 cm以下 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 日 期 | 4月10日 | 4月11日 | 4月12日 | 4月13日 | 4月14日 |
| 温 差x(oC) | 10 | 12 | 13 | 14 | 11 |
| 发芽数y(颗) | 11 | 13 | 14 | 16 | 12 |
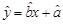 .
.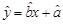 ,其中
,其中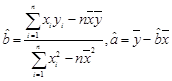 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com