练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知A、B、C是△ABC的三个内角,且满足(sinA+sinB)2-sin2C=3sinAsinB,求证:A+B=120°

       

    思路分析:由于A+B+C=180°,所以可将证明A+B=120°转化到证明C=60°上来.又已知条件为三角函数关系,因此应考虑向三角函数方向转化.在(0°,180°)上,余弦函数严格单调,所以可证明cosC=,这就考虑余弦定理的推论cosC=,因此应首先把已知条件中角的关系转化为边的关系.

        证明:由(sinA+sinB)2-sin2C=3sinAsinB,可得

    sin2A+sin2B-sin2C=sinAsinB,

        又∵sinA=,sinB=,sinC=,

    ∴+-=·,

        即a2+b2-c2=ab.

    ∴cosC===.

        又∵0°＜C＜180°,∴C=60°.

    ∴A+B=180°-C=120°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    3、已知a，b，c是三条不同的直线，α，β，γ是三个不同的平面，下列命题中正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A、B、C是直线l上的三点，向量
    OA
    、
    OB
    、
    OC
    满足
    OA
    -（y+1-lnx）
    OB
    +
    1-x
    ax
    OC
    =
    o
    ，（O不在直线l上a＞0）
    （1）求y=f（x）的表达式；
    （2）若函数f（x）在[1，∞]上为增函数，求a的范围；
    （3）当a=1时，求证lnn＞
    1
    2
    +
    1
    3
    +
    1
    4
    +…+
    1
    n
    ，对n≥2的正整数n成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a，b，c是直角三角形的三边，其中c为斜边，若实数M使不等式
    1
    a
    +
    1
    b
    +
    1
    c
    ≥
    M
    a+b+c
    恒成立，则实数M的最大值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知A、B、C是锐角△ABC的三个内角，内量p＝(1+sinA，1+cosA)，q＝(1+sinB，-1-cosB)，则p与q的夹角是


    1. A.
      锐角
    2. B.
      钝角
    3. C.
      直角
    4. D.
      不确定

    查看答案和解析>>

    科目：高中数学 来源：0119 期末题 题型：单选题

    已知a、b、c是直线，α、β是平面，给出下列五种说法：
    ①若a⊥b，b⊥c，则a∥c；   ②若a∥b，b⊥c，则a⊥c；
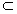    ③若a∥β，bβ，则a∥b； ④若a与b异面，且a∥β，则b与β相交；
    ⑤若a∥c，α∥β，a⊥α，则c⊥β。
    其中正确说法的个数是

    [     ]

    A．4
    B．3
    C．2
    D．1

    查看答案和解析>>

    同步练习册答案