解:(1)设椭圆的方程为mx
2+ny
2=1,
因为椭圆经过两点M(1,

),N(-

,

),
所以可得
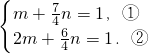
由①与②消去m可得n=

,③
将③代入①得m=

,
故所求椭圆的标准方程为
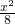
+

=1.
抛物线C:x
2=2py(p>0)的焦点为F(0,

),依题意得直线FP与直线l:x-y-2=0互相垂直,所以直线FP的斜率为-1,则k
FP=
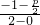
=-1,解得p=2,所以x
2=4y.
(2)由
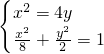
得y
2+y-2=0,解得y=1或y=-2(不合题意,舍去),
当y=1时,得x=±2,因为x
A<x
B,所以A(-2,1),对y=

x
2求导,得y′=

x,所以y′|
x=-2=-1,所以直线l′的方程为y-1=-1×(x+2),即x+y+1=0,令x=0得y=-1,令y=0得x=-1,所以直线l′与坐标轴所围成的三角形的面积为S=

×|-1|×|-1|=

.
(3)由x
2-2mx+y
2+2y+m
2-

=0得(x-m)
2+(y+1)
2=

,其圆心坐标为(m,-1),半径r=

,
要使直线l′与圆x
2-2mx+y
2+2y+m
2-

=0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤

,即d=
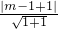
≤

,得-
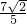
≤m≤
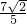
,
即m的取值范围为[-
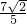
,
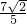
].
分析:(1)设椭圆的方程为mx
2+ny
2=1,因为椭圆经过两点M(1,

),N(-

,

),所以可得
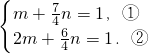
由①与②消去m可得n=

,由此能求出抛物线方程与椭圆的标准方程.
(2)由
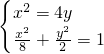
得y
2+y-2=0,解得y=1或y=-2(不合题意,舍去),当y=1时,得x=±2,因为x
A<x
B,所以A(-2,1),对y=

x
2求导,得y′=

x,所以直线l′的方程为x+y+1=0,由此能求出直线l′与坐标轴所围成的三角形的面积.
(3)由x
2-2mx+y
2+2y+m
2-

=0得(x-m)
2+(y+1)
2=

,其圆心坐标为(m,-1),半径r=

,要使直线l′与圆x
2-2mx+y
2+2y+m
2-

=0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤

,由此能求出m的取值范围.
点评:本题考查直线 与圆锥曲线的位置关系的综合运用,具有一定的难度,解题时要认真审题,合理地进行等价转化.

 ),N(-
),N(- ,
, ),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB.
),且抛物线与椭圆交于两点A(xA,yA)和B(xB,yB),且xA<xB. =0恒有公共点,试求m的取值范围.
=0恒有公共点,试求m的取值范围. ),N(-
),N(- ,
, ),
),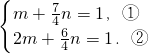
 ,③
,③ ,
,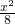 +
+ =1.
=1. ),依题意得直线FP与直线l:x-y-2=0互相垂直,所以直线FP的斜率为-1,则kFP=
),依题意得直线FP与直线l:x-y-2=0互相垂直,所以直线FP的斜率为-1,则kFP=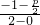 =-1,解得p=2,所以x2=4y.
=-1,解得p=2,所以x2=4y.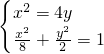 得y2+y-2=0,解得y=1或y=-2(不合题意,舍去),
得y2+y-2=0,解得y=1或y=-2(不合题意,舍去), x2求导,得y′=
x2求导,得y′= x,所以y′|x=-2=-1,所以直线l′的方程为y-1=-1×(x+2),即x+y+1=0,令x=0得y=-1,令y=0得x=-1,所以直线l′与坐标轴所围成的三角形的面积为S=
x,所以y′|x=-2=-1,所以直线l′的方程为y-1=-1×(x+2),即x+y+1=0,令x=0得y=-1,令y=0得x=-1,所以直线l′与坐标轴所围成的三角形的面积为S= ×|-1|×|-1|=
×|-1|×|-1|= .
. =0得(x-m)2+(y+1)2=
=0得(x-m)2+(y+1)2= ,其圆心坐标为(m,-1),半径r=
,其圆心坐标为(m,-1),半径r= ,
, =0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤
=0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤ ,即d=
,即d=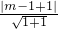 ≤
≤ ,得-
,得-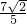 ≤m≤
≤m≤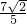 ,
,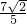 ,
,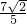 ].
]. ),N(-
),N(- ,
, ),所以可得
),所以可得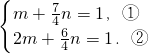
 ,由此能求出抛物线方程与椭圆的标准方程.
,由此能求出抛物线方程与椭圆的标准方程.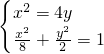 得y2+y-2=0,解得y=1或y=-2(不合题意,舍去),当y=1时,得x=±2,因为xA<xB,所以A(-2,1),对y=
得y2+y-2=0,解得y=1或y=-2(不合题意,舍去),当y=1时,得x=±2,因为xA<xB,所以A(-2,1),对y= x2求导,得y′=
x2求导,得y′= x,所以直线l′的方程为x+y+1=0,由此能求出直线l′与坐标轴所围成的三角形的面积.
x,所以直线l′的方程为x+y+1=0,由此能求出直线l′与坐标轴所围成的三角形的面积. =0得(x-m)2+(y+1)2=
=0得(x-m)2+(y+1)2= ,其圆心坐标为(m,-1),半径r=
,其圆心坐标为(m,-1),半径r= ,要使直线l′与圆x2-2mx+y2+2y+m2-
,要使直线l′与圆x2-2mx+y2+2y+m2- =0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤
=0恒有公共点,则需满足(m,-1)到直线l′:x+y+1=0的距离d≤ ,由此能求出m的取值范围.
,由此能求出m的取值范围.
