
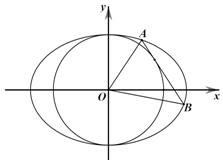
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2分析 (1)利用椭圆经过的点代入椭圆方程,求出a,b即可求解椭圆方程.
(2)设直线l为y=kx+m(k<0,m>0),联立$\left\{\begin{array}{l}{x^2}+2{y^2}=2\\ y=kx+m\end{array}\right.$,消去y,设x1,x2分别为A、B横坐标,利用韦达定理弦长公式点到直线的距离公式,通过三角形的面积,求解即可.
解答 (本小题满分14分)
解:(1)$\left\{\begin{array}{l}\frac{0^2}{a^2}+\frac{1^2}{b^2}=1\\ \frac{1^2}{a^2}+\frac{1}{{2{b^2}}}=1\end{array}\right.⇒\left\{\begin{array}{l}a=\sqrt{2}\\ b=1\end{array}\right.$,
椭圆方程为:$\frac{x^2}{2}+{y^2}=1$…(4分)
(2)因为切点在第一象限,可设直线l为y=kx+m(k<0,m>0),
联立方程$\left\{\begin{array}{l}{x^2}+2{y^2}=2\\ y=kx+m\end{array}\right.$,
得$(1+2{k^2}){x^2}+4kmx+2{m^2}-2=0⇒\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}\\{x_1}{x_2}=\frac{{2{m^2}-2}}{{1+2{k^2}}}\end{array}\right.$(x1,x2分别为A、B横坐标)$d=\frac{|m|}{{\sqrt{1+{k^2}}}}=1⇒{m^2}=1+{k^2}$…(8分)
AB长:${l_{AB}}=\sqrt{1+{k^2}}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{1+{k^2}}•\sqrt{{{(\frac{4km}{{1+2{k^2}}})}^2}-4\frac{{2{m^2}-2}}{{1+2{k^2}}}}$
=$\frac{{2\sqrt{2}•\sqrt{1+{k^2}}}}{{1+2{k^2}}}•\sqrt{k^2}$…(10分)
∴$S=\frac{1}{2}{l_{AB}}•d=\frac{1}{2}•1•\frac{{2\sqrt{2}•\sqrt{1+{k^2}}}}{{1+2{k^2}}}•\sqrt{k^2}=\frac{{\sqrt{6}}}{4}⇒\frac{{(1+{k^2})•{k^2}}}{{(1+2{k^2}{)^2}}}=\frac{3}{16}$∴$16(1+{k^2})•{k^2}=3(1+2{k^2}{)^2}⇒(2{k^2}+3)(2{k^2}-1)=0⇒{k^2}=\frac{1}{2}⇒k=-\frac{{\sqrt{2}}}{2}$…(12分)
∴m=$\sqrt{1+{k}^{2}}$=$\frac{\sqrt{6}}{2}$,直线l为$y=-\frac{{\sqrt{2}}}{2}x+\frac{{\sqrt{6}}}{2}$…(14分)
点评 本题考查椭圆的简单性质椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}π}}{5}$ | B. | $\frac{{4\sqrt{5}π}}{5}$ | C. | $\frac{{2\sqrt{10}π}}{5}$ | D. | $\frac{{4\sqrt{10}π}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{DA}$ | D. | $\overrightarrow 0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{3}$x | C. | y=±x | D. | y=±$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\overrightarrow{OC}$ | B. | $\overrightarrow{OD}$ | C. | $\overrightarrow{OB}$ | D. | $\overrightarrow{CO}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com