
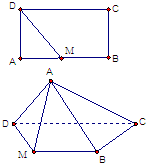
 如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| ||
| 4 |
| ||
| 8 |


科目:高中数学 来源: 题型:
A.![]() (5e1+3e2) B.
(5e1+3e2) B.![]() (5e1-3e2)
(5e1-3e2)
C.![]() (3e2+5e1) D.
(3e2+5e1) D.![]() (5e2-3e1)
(5e2-3e1)
查看答案和解析>>
科目:高中数学 来源: 题型:
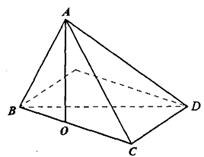 如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
△ABD折起,使A点在平面BCD内的射影落在
BC边上,若二面角C—AB—D的平面有大小为
θ,则sinθ
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练6练习卷(解析版) 题型:选择题
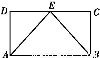
如图,矩形ABCD中,点E为边CD的中点.若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于( )
(A) 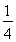 (B)
(B) 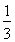 (C)
(C) 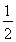 (D)
(D) 
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三上学期第二次模拟理科数学试卷(解析版) 题型:填空题
如图:矩形ABCD中,AB= BC=2 点E为BC的中点,点F在CD上。若
BC=2 点E为BC的中点,点F在CD上。若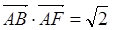 则
则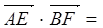 _____________。
_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com