
【题目】在三棱锥![]() 中,OA、OB、OC所在直线两两垂直,且
中,OA、OB、OC所在直线两两垂直,且![]() ,CA与平面AOB所成角为
,CA与平面AOB所成角为![]() ,D是AB中点,三棱锥
,D是AB中点,三棱锥![]() 的体积是
的体积是![]() .
.
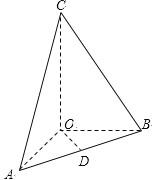
(1)求三棱锥![]() 的高;
的高;
(2)在线段CA上取一点E,当E在什么位置时,异面直线BE与OD所成的角为![]() ?
?
科目:高中数学 来源: 题型:
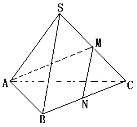
【题目】如图,在三棱锥![]() 中,若底面
中,若底面![]() 是正三角形,侧棱长
是正三角形,侧棱长![]() ,
,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,并且
的中点,并且![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角为______;三棱锥
所成角为______;三棱锥![]() 的外接球的体积为______.
的外接球的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 满足
满足![]() ,且
,且![]() ,
,![]() 分别是定义在
分别是定义在![]() 上的偶函数和奇函数.
上的偶函数和奇函数.
(1)求函数![]() 的反函数;
的反函数;
(2)已知![]() ,若函数
,若函数![]() 在
在![]() 上满足
上满足![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)若对于任意![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,沿
边的中点,沿![]() 将
将![]() 折起使得平面
折起使得平面![]() 平面
平面![]() .
.
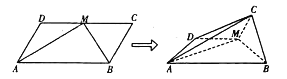
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)求折后直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() ,
,![]() 与
与![]() 关于抛物线的对称轴对称,斜率为1的直线交抛物线于
关于抛物线的对称轴对称,斜率为1的直线交抛物线于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 在直线
在直线![]() 两侧.
两侧.
(1)求证:![]() 平分
平分![]() ;
;
(2)点![]() 为抛物线在
为抛物线在![]() 、
、![]() 处切线的交点,若
处切线的交点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com