
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325 8430 8215 7453 7446 6754
7638 6834 6460 6830 9860 8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为![]() )
)
组别 | 步数分组 | 频数 |
|
| 2 |
|
| 10 |
|
|
|
|
| 2 |
|
|
|
(Ⅰ)写出![]() 的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,
,![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,试分别比较
,试分别比较![]() 与以
与以![]() ,
,![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述![]() 两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为
两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:
对于任意![]() ,都有
,都有![]() 成立.
成立.
①求数列![]() 的通项公式;
的通项公式;
②设数列![]() ,问:数列
,问:数列![]() 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 、
、![]() 为线段
为线段![]() 上的点,
上的点,![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起(如图2)
折起(如图2)
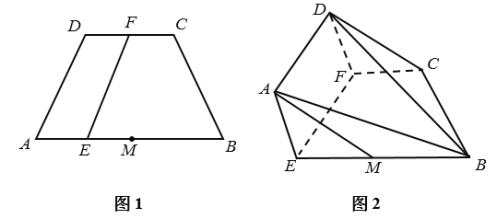
(1)求证:![]() 平面
平面![]() ;
;
(2)在图2中,若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 长轴的左、右端点,
长轴的左、右端点,![]() 为椭圆上的动点.
为椭圆上的动点.
(1)求![]() 的最大值,并证明你的结论;
的最大值,并证明你的结论;
(2)设直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家统计局数据,1978年至2018年我国GDP总量从0.37万亿元跃升至90万亿元,实际增长了242倍多,综合国力大幅提升.
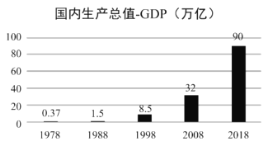
将年份1978,1988,1998,2008,2018分别用1,2,3,4,5代替,并表示为![]() ;
;![]() 表示全国GDP总量,表中
表示全国GDP总量,表中![]() ,
,![]() .
.
|
|
|
|
|
|
3 | 26.474 | 1.903 | 10 | 209.76 | 14.05 |
(1)根据数据及统计图表,判断![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为全国GDP总量
为自然对数的底数)哪一个更适宜作为全国GDP总量![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由),并求出
的回归方程类型?(给出判断即可,不必说明理由),并求出![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)使用参考数据,估计2020年的全国GDP总量.
线性回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
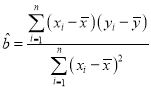 ,
,![]() .
.
参考数据:
| 4 | 5 | 6 | 7 | 8 |
| 55 | 148 | 403 | 1097 | 2981 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com