
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(![]() )若直线
)若直线![]() 的斜率为
的斜率为![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
(![]() )若函数
)若函数![]() 是区间
是区间![]() 上的单调函数,求
上的单调函数,求![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ;(2)
;(2)![]() 或
或![]()
【解析】试题分析:(1)求得![]() 的导数,可得切线的斜率,由条件可得
的导数,可得切线的斜率,由条件可得![]() ,由导数大于0,可得增区间,由导数小于0,可得减区间;(2)由题意可得当函数在
,由导数大于0,可得增区间,由导数小于0,可得减区间;(2)由题意可得当函数在![]() 递增(或递减),即有
递增(或递减),即有![]() 或
或![]() )对
)对![]() 成立,只要
成立,只要![]() 在
在![]() 上的最小值(或最大值)大于等于0即可.求出二次函数的对称轴,讨论区间
上的最小值(或最大值)大于等于0即可.求出二次函数的对称轴,讨论区间![]() 和对称轴的关系,求得最小值(或最大值),解不等式即可得到所求范围.
和对称轴的关系,求得最小值(或最大值),解不等式即可得到所求范围.
试题解析:(![]() )由
)由![]() 得
得![]() ,
,
若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的斜率为
的斜率为![]() ,
,
则![]() ,
,
∴![]() ,
, ![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;
;
令![]() ,得
,得![]() ,
,
∴函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() .
.
(![]() )①当函数
)①当函数![]() 在区间
在区间![]() 上单调递减时,
上单调递减时, ![]() 对
对![]() 成立,
成立,
即![]() 对
对![]() 成立,
成立,
根据二次函数的性质,只需要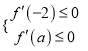 ,
,
解得![]() ,
,
又![]() ,所以
,所以![]() ;
;
②当函数![]() 在区间
在区间![]() 上单调递增时,
上单调递增时, ![]() 对
对![]() 成立,
成立,
只需![]() 在
在![]() 上的最小值大于等于
上的最小值大于等于![]() 即可,
即可,
函数![]() 的对称轴为
的对称轴为![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
∴![]() ,解得
,解得![]() 或
或![]() ,
,
此种情形不成立;
当![]() 时,
时, ![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
∴![]() ,解得
,解得![]() ;
;
综上所述,实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用![]() (单位:万元)和产品营业额
(单位:万元)和产品营业额![]() (单位:万元)的统计折线图.
(单位:万元)的统计折线图.

(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用![]() 与产品营业额
与产品营业额![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立产品营业额![]() 关于宣传费用
关于宣传费用![]() 的归方程;
的归方程;
(Ⅲ)若某段时间内产品利润![]() 与宣传费
与宣传费![]() 和营业额
和营业额![]() 的关系为
的关系为![]() ,应投入宣传费多少万元才能使利润最大,并求最大利润.
,应投入宣传费多少万元才能使利润最大,并求最大利润.
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, 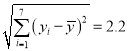 ,
, ![]()
参考公式:相关系数, 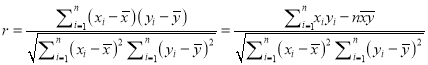 ,
,
回归方程![]() 中斜率和截距的最小二乘佔计公式分别为
中斜率和截距的最小二乘佔计公式分别为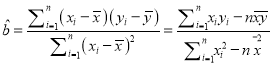 ,
, ![]() .(计算结果保留两位小数)
.(计算结果保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数的比为
内的男生数与女生数的比为![]() ,若在满意度评分值为
,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,圆
,圆![]() 上的动点T满足:线段TQ的垂直平分线与线段TP相交于点K.
上的动点T满足:线段TQ的垂直平分线与线段TP相交于点K.
![]() Ⅰ
Ⅰ![]() 求点K的轨迹C的方程;
求点K的轨迹C的方程;
![]() Ⅱ
Ⅱ![]() 经过点
经过点![]() 的斜率之积为
的斜率之积为![]() 的两条直线,分别与曲线C相交于M,N两点,试判断直线MN是否经过定点
的两条直线,分别与曲线C相交于M,N两点,试判断直线MN是否经过定点![]() 若是,则求出定点坐标;若否,则说明理由.
若是,则求出定点坐标;若否,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图
(如图![]() ).
).


图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中有![]() 个大小之地都相同的小球,其中红球
个大小之地都相同的小球,其中红球![]() 个,白球
个,白球![]() 个,黑球
个,黑球![]() 个,现从袋中有放回的取球,每次随机取一个,连续取两次.
个,现从袋中有放回的取球,每次随机取一个,连续取两次.
(1)设![]() 表示先后两次所取到的球,试写出所有可能抽取结果;
表示先后两次所取到的球,试写出所有可能抽取结果;
(2)求连续两次都取到白球的概率;
(3)若取到红球记![]() 分,取到白球记
分,取到白球记![]() 分,取到黑球记
分,取到黑球记![]() 分,求连续两次球所得总分数大于
分,求连续两次球所得总分数大于![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com