
【题目】一汽车厂生产![]() ,
,![]() ,
,![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() ,记这8辆轿车的得分的平均数为
,记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() ,且函数
,且函数![]() 没有零点
没有零点![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() ,
,![]() 为
为![]() 的焦点,
的焦点,![]() 为准线,且
为准线,且![]() 与
与![]() 轴的交点为
轴的交点为![]() .过点
.过点![]() 任意作一条直线交抛物线
任意作一条直线交抛物线![]() 于
于![]() 两点.
两点.
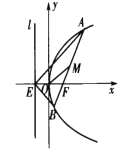
(1)若![]()
![]() ,求证:
,求证:![]() ;
;
(2)设![]() 为线段
为线段![]() 的中点,
的中点,![]() 为奇质数,且点
为奇质数,且点![]() 到
到![]() 轴的距离和点
轴的距离和点![]() 到准线
到准线![]() 的距离均为非零整数.求证:点
的距离均为非零整数.求证:点![]() 到坐标原点
到坐标原点![]() 的距离不可能是整数.
的距离不可能是整数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一张长为12,宽为8的铁皮围成圆柱形的侧面,则这个圆柱的体积为_____;半径为R的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c,且![]() .
.
(1)求角A;
(2)若△ABC外接圆的面积为4π,且△ABC的面积![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com