
 和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在
和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在 上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在
上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.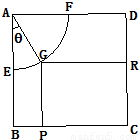
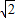 sin(θ+45°),则sinθcosθ=
sin(θ+45°),则sinθcosθ=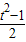 ,
,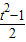 =
= (t-2)2+
(t-2)2+ .
.
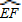 的中点,矩形面积最大值为2.
的中点,矩形面积最大值为2.

科目:高中数学 来源: 题型:
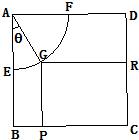 现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形
现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形 |
| AEF |
 |
| EF |
 |
| EF |
查看答案和解析>>
科目:高中数学 来源:2010-2011辽宁省大连市协作体高一4月月考数学理卷 题型:解答题
((本小题满分12分)
现将边长为2米的正方形铁片 裁剪成一个半径为1米的扇形
裁剪成一个半径为1米的扇形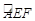 和一个矩形
和一个矩形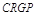 ,如图所示,点
,如图所示,点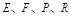 分别在
分别在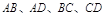 上,点
上,点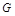 在
在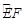 上.设矩形
上.设矩形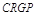 的面积为
的面积为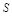 ,
,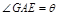 ,试将
,试将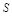 表示为
表示为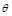 的函数,并指出点
的函数,并指出点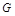 在
在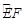 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.
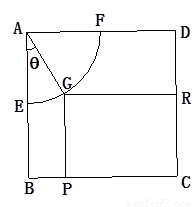
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
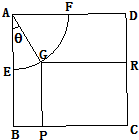 现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形
现将边长为2米的正方形铁片ABCD裁剪成一个半径为1米的扇形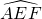 和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在
和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在 上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在
上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省大连市协作体高一(下)4月月考数学试卷(理科)(解析版) 题型:解答题
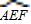 和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在
和一个矩形CRGP,如图所示,点E、F、P、R分别在AB、AD、BC、CD上,点G在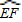 上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在
上.设矩形CRGP的面积为S,∠GAE=θ,试将S表示为θ的函数,并指出点G在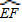 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.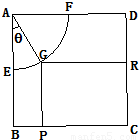
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com