
分析 函数f(x)是定义在R上的偶函数,实数b满足$2f({log_2}b)+f({log_{\frac{1}{2}}}b)≤3f(1)$,可得f(|log2b|)≤f(1),利用f(x)在区间[0,+∞)上单调递增,可得|log2b|≤1,即可求出实数b的取值范围.
解答 解:∵函数f(x)是定义在R上的偶函数,实数b满足$2f({log_2}b)+f({log_{\frac{1}{2}}}b)≤3f(1)$,
∴f(|log2b|)≤f(1),
∵f(x)在区间[0,+∞)上单调递增,
∴|log2b|≤1,
∴-1≤log2b≤1,
∴b∈$[{\frac{1}{2},2}]$,
故答案为$[{\frac{1}{2},2}]$.
点评 本题考查函数的性质和运用,考查函数的奇偶性、单调性和运用,考查对数不等式的解法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
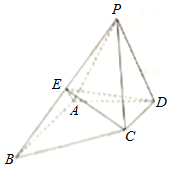 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com