
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|= ![]() |PQ|. (Ⅰ)求C的方程;
|PQ|. (Ⅰ)求C的方程;
(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.
【答案】解:(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C:y2=2px(p>0),
可得x0= ![]() ,∵点P(0,4),∴|PQ|=
,∵点P(0,4),∴|PQ|= ![]() .
.
又|QF|=x0+ ![]() =
= ![]() +
+ ![]() ,|QF|=
,|QF|= ![]() |PQ|,
|PQ|,
∴ ![]() +
+ ![]() =
= ![]() ×
× ![]() ,求得 p=2,或 p=﹣2(舍去).
,求得 p=2,或 p=﹣2(舍去).
故C的方程为 y2=4x.
(Ⅱ)由题意可得,直线l和坐标轴不垂直,y2=4x的焦点F(1,0),
设l的方程为 x=my+1(m≠0),
代入抛物线方程可得y2﹣4my﹣4=0,显然判别式△=16m2+16>0,y1+y2=4m,y1y2=﹣4.
∴AB的中点坐标为D(2m2+1,2m),弦长|AB|= ![]() |y1﹣y2|=
|y1﹣y2|= ![]() =4(m2+1).
=4(m2+1).
又直线l′的斜率为﹣m,∴直线l′的方程为 x=﹣ ![]() y+2m2+3.
y+2m2+3.
过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,
把线l′的方程代入抛物线方程可得 y2+ ![]() y﹣4(2m2+3)=0,∴y3+y4=
y﹣4(2m2+3)=0,∴y3+y4= ![]() ,y3y4=﹣4(2m2+3).
,y3y4=﹣4(2m2+3).
故线段MN的中点E的坐标为( ![]() +2m2+3,
+2m2+3, ![]() ),∴|MN|=
),∴|MN|= ![]() |y3﹣y4|=
|y3﹣y4|= 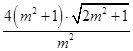 ,
,
∵MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|= ![]() |MN|,
|MN|,
∴ ![]() +DE2=
+DE2= ![]() MN2,
MN2,
∴4(m21)2 + ![]() +
+ ![]() =
= ![]() ×
× ![]() ,化简可得 m2﹣1=0,
,化简可得 m2﹣1=0,
∴m=±1,∴直线l的方程为 x﹣y﹣1=0,或 x+y﹣1=0
【解析】(Ⅰ)设点Q的坐标为(x0,4),把点Q的坐标代入抛物线C的方程,求得x0= ![]() ,根据|QF|=
,根据|QF|= ![]() |PQ|求得 p的值,可得C的方程.(Ⅱ)设l的方程为 x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|=
|PQ|求得 p的值,可得C的方程.(Ⅱ)设l的方程为 x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|= ![]() |MN|,由此求得m的值,可得直线l的方程.
|MN|,由此求得m的值,可得直线l的方程.


科目:高中数学 来源: 题型:
【题目】为了稳定市场,确保农民增收,某农产品7个月份的每月市场收购价格与其前三个月的市场收购价格有关,并使其与前三个月的市场收购价格之差的平方和最小,下表列出的是该产品今年前6个月的市场收购价格,则前7个月该产品的市场收购价格的方差为( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
A.![]()
B.![]()
C.11
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在直角梯形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .将
.将 ![]() 沿
沿 ![]() 折起,使得点
折起,使得点 ![]() 在平面
在平面 ![]() 的正投影
的正投影 ![]() 恰好落在
恰好落在 ![]() 边上,得到几何体
边上,得到几何体 ![]() ,如图2所示.
,如图2所示.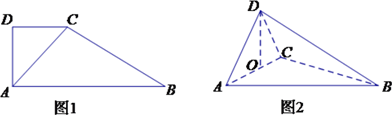
(1)求证: ![]() ;
;
(2)求点 ![]() 到平面
到平面 ![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.经过点P0(x0 , y0)的直线都可以用方程y-y0=k(x-x0)表示
B.经过定点A(0,b)的直线都可以用方程y=kx+b表示
C.经过任意两个不同点P1(x1 , y1),P2(x2 , y2)的直线都可用方程(x2-x1)(y-y1)=(y2-y1)(x-x1)表示
D.不经过原点的直线都可以用方程 ![]() 表示
表示
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是 ![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于 ![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
(1)求证: ![]()
(2)当三棱锥 ![]() 的体积最大时,求
的体积最大时,求 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点 ![]() ,使二面角
,使二面角 ![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时 ![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=f(x)、对数函数y=g(x)和幂函数y=h(x)的图象都经过点P( ![]() ),如果f(x1)=g(x2)=h(x3)=4,那么x1+x2+x3=( )
),如果f(x1)=g(x2)=h(x3)=4,那么x1+x2+x3=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com