
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式:
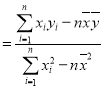 ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|-3≤x<3},B={x|2<x≤5},则A∪B=( )
A.{x|2<x<3}
B.{x|-3≤x≤5}
C.{x|-3<x<5}
D.{x|-3<x≤5}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若p,q为简单命题,则“p且q为假”是“p或q为假”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国人民代表大会在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名女记者担任对外翻译工作.调查发现,男、女记者中分别有10人和6人会俄语.
(1)根据以上数据完成以下![]() 列联表:
列联表:
会俄语 | 不会俄语 | 总计 | |
男 | |||
女 | |||
总计 |
(2)能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() , 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线.
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线.
(1)若抛物线C在点M的法线的斜率为![]() ,求点M的坐标
,求点M的坐标![]() ;
;
(2)设P![]() 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P.若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P.若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),变量U与V相对应的一组数据为 (10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
A.r2<r1<0 B.0<r2<r1
C.r2<0<r1 D.r2=r1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人坐飞机去外地办一件急事,下面是他自己从家里出发到坐在机舱内这一过程的主要算法:
S1 乘车去飞机场售票处;
S2 _____;
S3 凭票上机,对号入座.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com