
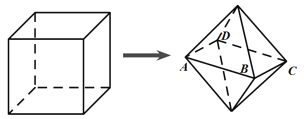
【题目】如图,棱长为1(单位:![]() )的正方体木块经过适当切割,得到几何体
)的正方体木块经过适当切割,得到几何体![]() ,已知几何体
,已知几何体![]() 由两个底面相同的正四棱锥组成,底面
由两个底面相同的正四棱锥组成,底面![]() 平行于正方体的下底面,且各顶点均在正方体的面上,则几何体
平行于正方体的下底面,且各顶点均在正方体的面上,则几何体![]() 体积的取值范围是________(单位:
体积的取值范围是________(单位:![]() ).
).
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,CD⊥AD,BC∥AD,
中,PA⊥平面ABCD,CD⊥AD,BC∥AD,![]() .
.

(Ⅰ)求证:CD⊥PD;
(Ⅱ)求证:BD⊥平面PAB;
(Ⅲ)在棱PD上是否存在点M,使CM∥平面PAB,若存在,确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道测试题,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为![]() .假设甲、乙两名学生解答每道测试题都相互独立,互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答.
.假设甲、乙两名学生解答每道测试题都相互独立,互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答.
(1)求甲、乙两名学生共答对2道测试题的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点
=1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点 ![]() .
.
(1)求椭圆C的方程;
(2)设M,N为椭圆C上不同的两点,A,B分别为椭圆C上的左右顶点,直线MN既不平行与坐标轴,也不过椭圆C的右焦点F,若∠AFM=∠BFN,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最小值为60°;
其中正确的是(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
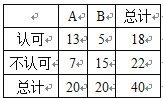
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:
附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com