
【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距 ![]() km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 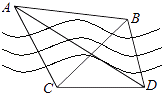
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() 相交于
相交于![]() ,
, ![]() ,点
,点![]() 在平面
在平面![]() 上的射影恰好是线段
上的射影恰好是线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),设
=(cosα,sinα),设 ![]() =
= ![]() ﹣t
﹣t ![]() (t为实数).
(t为实数).
(1)t=1 时,若 ![]() ∥
∥ ![]() ,求2cos2α﹣sin2α的值;
,求2cos2α﹣sin2α的值;
(2)若α= ![]() ,求|
,求| ![]() |的最小值,并求出此时向量
|的最小值,并求出此时向量 ![]() 在
在 ![]() 方向上的投影.
方向上的投影.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() (
(![]() )的一条直线的两个端点.
)的一条直线的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 两点,射线
两点,射线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() ,试探究:是否存在数集
,试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.

(1)当θ=![]() 时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;
时,求点A的位置,使矩形ABOC的面积最大,并求出这个最大面积;
(2)当θ=![]() 时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.
时,求点A的位置,使平行四边形ABOC的面积最大,并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现阶段全国多地空气质量指数“爆表”.为探究车流量与![]() 浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到
浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到![]() 月某天
月某天![]() 个不同时段车流量与
个不同时段车流量与![]() 浓度的数据,如下表:
浓度的数据,如下表:
车流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)规定当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为优;当
,空气质量等级为优;当![]() 浓度平均值在
浓度平均值在![]() ,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
,空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程: ![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com