
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,三角形
,三角形![]() 是等边三角形,平面
是等边三角形,平面![]() 平面
平面![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.
的中点.
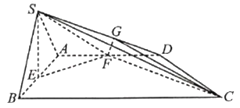
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
【答案】(1)证明见解析(2)![]()
【解析】
(1)由平面![]() 平面
平面![]() ,可以得到
,可以得到![]() ,连接
,连接![]() ,由角的关系可求出
,由角的关系可求出![]() ,由线面垂直的判定定理可以得到
,由线面垂直的判定定理可以得到![]() 平面
平面![]() ,进而求出平面
,进而求出平面![]() 平面
平面![]() ;
;
(2)过E作![]() ,则
,则![]() ,
,![]() ,
,![]() 两两垂直,由此可建立空间直角坐标系,利用向量法求直线
两两垂直,由此可建立空间直角坐标系,利用向量法求直线![]() 与平面
与平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
(1)三角形![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
连接![]() ,因为E,F分别为
,因为E,F分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() .
.
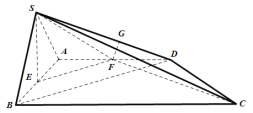
因为![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)过E作![]() ,则
,则![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
故可如图建立空间直角坐标系.
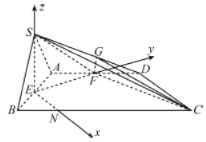
在![]() 中,易求得
中,易求得![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,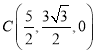 ,
,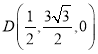 .
.
故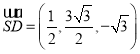 ,
,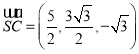 ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,可取
,可取![]() .
.
则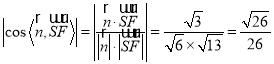 .
.
故![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为
的回归方程,并预测液体肥料每亩使用量为![]() 千克时,西红柿亩产量的增加量约为多少?
千克时,西红柿亩产量的增加量约为多少?
附:相关系数公式 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产能利用率是工业总产出对生产设备的比率,反映了实际生产能力到底有多少在运转发挥生产作用.汽车制造业的产能利用率的正常值区间为![]() ,称为“安全线”.如图是2017年第3季度到2019年第4季度的中国汽车制造业的产能利用率的统计图.以下结论正确的是( )
,称为“安全线”.如图是2017年第3季度到2019年第4季度的中国汽车制造业的产能利用率的统计图.以下结论正确的是( )
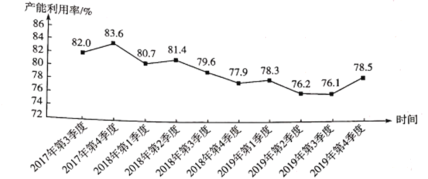
A.10个季度中,汽车产能利用率低于“安全线”的季度有5个
B.10个季度中,汽车产能利用率的中位数为![]()
C.2018年4个季度的汽车产能利用率的平均数为![]()
D.与上一季度相比,汽车产能利用率变化最大的是2019年第4季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ:![]() 的离心率为
的离心率为![]() ,左右焦点分别为F1,F2,且A、B分别是其左右顶点,P是椭圆上任意一点,△PF1F2面积的最大值为4.
,左右焦点分别为F1,F2,且A、B分别是其左右顶点,P是椭圆上任意一点,△PF1F2面积的最大值为4.
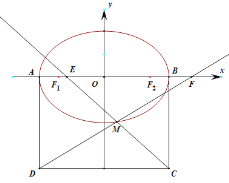
(1)求椭圆Γ的方程.
(2)如图,四边形ABCD为矩形,设M为椭圆Γ上任意一点,直线MC、MD分别交x轴于E、F,且满足![]() ,求证:AB=2AD.
,求证:AB=2AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,动点P为平面上一个动点,且直线SP,TP的斜率之积为
,动点P为平面上一个动点,且直线SP,TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在斜率为![]() 直线l,使得l交轨迹E于M,N两点,且
直线l,使得l交轨迹E于M,N两点,且![]() 恰是
恰是![]() 的重心?若存在,求l的方程;若不存在,说明理由.
的重心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式,使用提水吊杆——桔槔,后发展成辘轳.19世纪末,由于电动机的发明,离心泵得到了广泛应用,为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影,在A处测得B处的仰角为37度,在A处测得C处的仰角为45度,在B处测得C处的仰角为53度,A点所在等高线值为20米,若BC管道长为50米,则B点所在等高线值为( )(参考数据![]() )
)
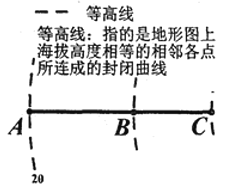
A.30米B.50米C.60米D.70米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障某种药品的主要药理成分在国家药品监督管理局规定的值范围内,某制药厂在该药品的生产过程中,检验员在一天中按照规定每间隔2小时对该药品进行检测,每天检测4次:每次检测由检验员从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:![]() )根据生产经验,可以认为这条药品生产线正常状态下生产的产品的其主要药理成分含量服从正态分布
)根据生产经验,可以认为这条药品生产线正常状态下生产的产品的其主要药理成分含量服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示某次抽取的20件产品中其主要药理成分含量在
表示某次抽取的20件产品中其主要药理成分含量在![]() 之外的药品件数,求
之外的药品件数,求![]() 的数学期望;
的数学期望;
(2)在一天的四次检测中,如果有一次出现了主要药理成分含量在![]() 之外的药品,就认为这条生产线在这一天的生产过程可能出现异常情况,需对本次的生产过程进行检查;如果有两次或两次以上出现了主要药理成分含量在
之外的药品,就认为这条生产线在这一天的生产过程可能出现异常情况,需对本次的生产过程进行检查;如果有两次或两次以上出现了主要药理成分含量在![]() 之外的药品,则需停止生产并对原材料进行检测.
之外的药品,则需停止生产并对原材料进行检测.
①下面是检验员在某次抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得,![]() ,
, .其中
.其中![]() 为抽取的第
为抽取的第![]() 件药品的主要药理成分含量
件药品的主要药理成分含量![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
②试确定一天中需停止生产并对原材料进行检测的概率(精确到0.001).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com