
【题目】数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)令![]() ,求数列
,求数列![]() 的最大值与最小值.
的最大值与最小值.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
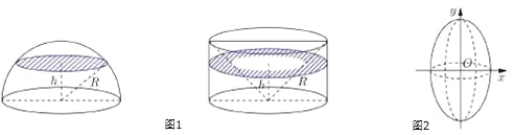
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
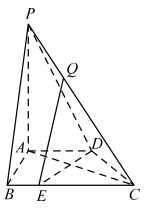
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将直线l沿x轴正方向平移3个单位长度,沿y轴正方向平移5个单位长度,得到直线l1.再将直线l1沿x轴正方向平移1个单位长度,沿y轴负方向平移2个单位长度,又与直线l重合.若直线l与直线l1关于点(2,3)对称,则直线l的方程是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)求证:![]() 在区间
在区间![]() 上单调递增;并求
上单调递增;并求![]() 在区间
在区间![]() 的反函数;
的反函数;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意可求得![]() ,则
,则![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
当直线![]() 的斜率不存在或直线
的斜率不存在或直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程,结合韦达定理计算可得直线
,联立直线方程与椭圆方程,结合韦达定理计算可得直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() .综上可得:直线
.综上可得:直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(Ⅰ)设![]() 由题
由题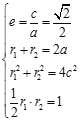 ,
,
解得![]() ,则
,则![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率不存在时,
的斜率不存在时,
设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() 代入
代入![]() ,
,
可得![]()
![]() ,
,![]() ,则
,则![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,
则由 消去
消去![]() 可得:
可得:![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得:
,代入上述方程可得:
![]() ,
,![]() ,
,
则![]()
![]() ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]()
 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【点睛】
(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.
【题型】解答题
【结束】
21
【题目】已知函数f(x)=(x+b)(![]() -a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
-a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(Ⅰ)求a,b;
(Ⅱ)若方程f(x)=m有两个实数根x1,x2,且x1<x2,证明:x2-x1≤1+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)证明:数列![]() 是等差数列,并写出其通项公式;
是等差数列,并写出其通项公式;
(3)设![]() (
(![]() ),试问是否存在正整数
),试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点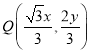 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆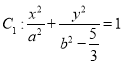 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆的一个顶点,△
是椭圆的一个顶点,△![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上一动点,求线段
上一动点,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 分别作直线
分别作直线![]() ,
,![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为![]() ,
,![]() ,
,
且![]() ,探究:直线
,探究:直线![]() 是否过定点,并说明理由.
是否过定点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com