
����Ŀ����������˾Ϊ�˵���A��B���ֳ��͵ij���������������ȡ�������ֳ���100���������ֱ�ͳ����ÿ����ij�������ڵij���������ͳ���������±��� A�ͳ�
�������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
������ | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B�ͳ�
�������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
������ | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
�� I���ӳ�������Ϊ3�������������A��B���ֳ��ͣ��������ȡһ����������������ǡ����A�ͳ��ĸ��ʣ�
������������ڵ�ͳ�����ݣ����Ƹù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ��ʣ�
����������ֳ���ÿ����ÿ������õ�������ͬ���ù�˾��Ҫ��A��B���ֳ����й���һ�������������ѧ��ͳ��֪ʶ����������Ӧ�ù�����һ�ֳ��ͣ���˵��������ɣ�
���𰸡��⣺�� I���߳�������Ϊ3�������A�ͳ���30����B�ͳ�20�������������ȡһ��������������A�ͳ��ĸ���ԼΪ ![]() =0.6��
=0.6��
�� II���衰�¼�Ai��ʾһ��A�ͳ���һ���ڳ�������ǡ��Ϊi�족��
���¼�Bj��ʾһ��B�ͳ���һ���ڳ�������ǡ��Ϊj�족������i��j=1��2������7��
��ù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ���Ϊ
P��A1B3+A2B2+A3B1��=P��A1B3��+P��A2B2��+P��A3B1��
=P��A1��P��B3��+P��A2��P��B2��+P��A3��P��B1��
= ![]()
= ![]() ��
��
�ù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ���Ϊ ![]() ��
��
������XΪA�ͳ��������������X�ķֲ���Ϊ
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P | 0.05 | 0.10 | 0.30 | 0.35 | 0.15 | 0.03 | 0.02 |
��YΪB�ͳ��������������Y�ķֲ���Ϊ
Y | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P | 0.14 | 0.20 | 0.20 | 0.16 | 0.15 | 0.10 | 0.05 |
E��X��=1��0.05+2��0.10+3��0.30+4��0.35+5��0.15+6��0.03+7��0.02=3.62��
E��Y��=1��0.14+2��0.20+3��0.20+4��0.16+5��0.15+6��0.10+7��0.05=3.48��
һ��A���͵ij��һ�����ڳ���������ƽ��ֵΪ3.62�죬B���һ�����ڳ���������ƽ��ֵΪ3.48�죮
�ӳ�������������������A�ͳ����������ķ������B�ͳ����������ķ���ۺϷ�����ѡ��A���͵ij�����Ӻ���
���������������ùŵ���͵ĸ��ʼ��㹫ʽ���ɵó������ù�˾һ��A�ͳ���һ��B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4���Ϊ�������������A�ͳ�1��B�ͳ�3�죻A�ͳ�B�ͳ���2�죻A�ͳ�3��B�ͳ�1�죬���û����¼��Ͷ����¼��ĸ��ʼ��㹫ʽ���ɵó���������ѧ�����ͷ���������ɵó����ۣ�
�����㾫����������ɢ�������������ֲ��ж���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x����ͼ�����y��Գƣ���x�ʣ�0��+�ޣ�ʱ��f��x��=log2x����a=f����3����b=f�� ![]() ����c=f��2������a��b��c�Ĵ�С��ϵ�ǣ� ��
����c=f��2������a��b��c�Ĵ�С��ϵ�ǣ� ��
A.a��b��c
B.b��a��c
C.c��a��b
D.a��c��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�Һ��ബO�������״������ⷶΧ�ǰ뾶Ϊ25 km��Բ��������һ���⼮�ִ���λ�ں��ബ����40 km��A����������ֱʻ��λ�ں��ബ����30 km��B���������ٶ�Ϊ28 km/h.
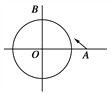
���������⼮�ִ��ܷ��ബ��������������ʱ����(Ҫ�������귨)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����[x]��ʾ������x������������磺[��]=3��[��4.3]=��5�������������⣺ �ٶ�����ʵ��x������[x]��x��0��
����x1��x2 �� ��[x1]��[x2]��
��[lg1]+[lg2]+[lg3]+��+[lg100]=90��
��������f��x��= ![]() ��
�� ![]() ����y=[f��x��]+[f����x��]��ֵ��Ϊ{��1��0}��
����y=[f��x��]+[f����x��]��ֵ��Ϊ{��1��0}��
�������������������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��mx��8y��n��0��l2��2x��my��1��0����ƽ������l1��l2֮��ľ���Ϊ![]() ����ֱ��l1�ķ��̣�
����ֱ��l1�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2��2ax��8a2��a��0�����Dz���ʽf��x����0�Ľ⼯ΪA��
��1����a=1ʱ����A��
��2��������1��1��A����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x3��2x+ex�� ![]() ������e����Ȼ�����ĵ�������f��a��1��+f��2a2����0����ʵ��a��ȡֵ��Χ�� ��
������e����Ȼ�����ĵ�������f��a��1��+f��2a2����0����ʵ��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
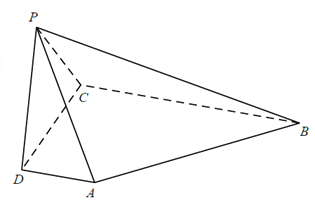
����Ŀ����ͼ��������![]() �У�
�У� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() .
.
��I��������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��II����֤�� ![]() ƽ��
ƽ��![]() ��
��
������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com