
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点
,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
① 向左平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
② 向右平移![]() 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的![]() ;
;
③ 每个点的横坐标缩短为原来的![]() ,向右平移
,向右平移![]() 个单位长度;
个单位长度;
④ 每个点的横坐标缩短为原来的![]() ,向左平移
,向左平移![]() 个单位长度;
个单位长度;
其中能将![]() 的图像变换成函数
的图像变换成函数![]() 的图像的是( )
的图像的是( )
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某几何体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 是直角梯形,
是直角梯形, ![]() 是直角,
是直角, ![]() ,
, ![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() .
.
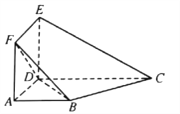
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的左焦点,离心率为
的左焦点,离心率为![]() ,直线
,直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中点,
的中点,![]() 是椭圆
是椭圆![]() 上一点,求
上一点,求![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前几年随着网购的普及,线下零售遭遇挑战,但随着新零售模式的不断出现,零售行业近几年呈现增长趋势,下表为![]() 年中国百货零售业销售额(单位:亿元,数据经过处理,
年中国百货零售业销售额(单位:亿元,数据经过处理, ![]() 分别对应
分别对应![]() ):
):
年份代码 | 1 | 2 | 3 | 4 |
销售额 | 95 | 165 | 230 | 310 |
(1)由上表数据可知,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,并预测2018年我国百货零售业销售额;
的回归方程,并预测2018年我国百货零售业销售额;
(3)从![]() 年这4年的百货零售业销售额及2018年预测销售额这5个数据中任取2个数据,求这2个数据之差的绝对值大于200亿元的概率.
年这4年的百货零售业销售额及2018年预测销售额这5个数据中任取2个数据,求这2个数据之差的绝对值大于200亿元的概率.
参考数据:
![]() ,
, 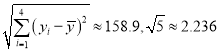
参考公式:相关系数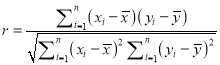 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为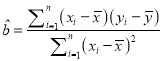 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2+ax-a),其中a是常数.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若存在实数k,使得关于x的方程f(x)=k在[0,+∞)上有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,![]() ,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,
,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,![]() ,则在这个红色子数列中,由1开始的第1000个数是_________
,则在这个红色子数列中,由1开始的第1000个数是_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com