
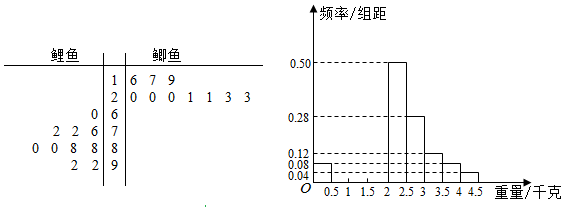
分析 (Ⅰ)根据茎叶图能求出有记号的鲤鱼和鲫鱼的平均数.
(Ⅱ)(1)根据题意,结合直方图确定频率,可将频率分布直方图补充完整.
(2)众数为2.25千克,中位数为2.02千克,平均数为2.02千克,可求鱼的总重.
解答 解:(Ⅰ)根据茎叶图可知,
鲤鱼的平均数目为:$\frac{1}{10}$(60+76+72+72+88+88+80+80+92+92)=80,
鲫鱼的平均数目为:$\frac{1}{10}(16+17+19+20+20+20+21+21+23+23)$=20.
(Ⅱ)(1)∵第二、三、四组鱼的条数成公差为7的等差数列,
设第二、三、四组的条数分别为x,x+7,x+14,
∴0.08×0.5+$\frac{x}{100}+\frac{x+7}{100}+\frac{x+14}{100}$+0.5×0.5+0.28×0.5+0.12×0.5+0.08×0.5+0.04×0.5=1,
解得x=8,∴第二、三、四组的频率分别为0.08、0.15、0.22,
可将频率分布直方图补充完整.
②∵区间[2,2.5)对应的小矩形最高,∴众数为2.25千克,
中位数为:2+$\frac{0.5-0.04-0.08-0.15-0.22}{0.25}×0.5$=2.02千克,
平均数为:0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+4.25×0.02=2.02千克,
所以鱼的总重为2.02×20000=40400千克.
点评 本题主要是考查了统计中茎叶图以及直方图和概率的求解运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{2}$ | B. | ±1 | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0>0,不等式x0-1≥lnx0成立 | B. | ?x0>0,不等式x0-1<lnx0成立 | ||
| C. | ?x≤0,不等式x-1≥lnx成立 | D. | ?x>0,不等式x-1<lnx成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
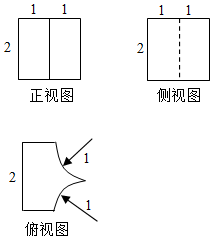 一个几何体的三视图如图所示,其中俯视图曲线部分是两个半径为1的圆弧,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图曲线部分是两个半径为1的圆弧,则这个几何体的体积是( )| A. | 8-$\frac{π}{4}$ | B. | 8-$\frac{π}{2}$ | C. | 8-π | D. | 8-2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | p∨(¬q) | D. | p∨q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com