
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点B(0,1).
,且过点B(0,1).

(Ⅰ)求椭圆的方程;
(Ⅱ)若点A是椭圆的右顶点,点![]() 在以AB为直径的圆上,延长PB交椭圆E于点Q,求
在以AB为直径的圆上,延长PB交椭圆E于点Q,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由椭圆的离心率和b=1,结合基本量的关系,可得a,进而得到椭圆方程;(Ⅱ)由A(2,0),又B(0,1),求得圆方程和设PQ的参数方程为![]() (t为参数,α为锐角),分别代入圆方程和椭圆方程,可得|BP|,|BQ|,再由换元法和判别式法,解不等式可得最大值.
(t为参数,α为锐角),分别代入圆方程和椭圆方程,可得|BP|,|BQ|,再由换元法和判别式法,解不等式可得最大值.
(Ⅰ)椭圆![]() 的离心率为
的离心率为![]() ,且过点B(0,1),可得b=1,
,且过点B(0,1),可得b=1,![]() ,
,![]() ,解得a=2,
,解得a=2,![]() ,则椭圆E的方程为
,则椭圆E的方程为![]() ;
;
(Ⅱ)可得A(2,0),又B(0,1),可得以AB为直径的圆方程为![]() ,
,
设PQ的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为锐角),
为锐角),
代入圆方程可得![]() ,
,
可得![]() ,
,
将直线的参数方程代入椭圆方程可得:
![]() ,
,
可得![]() ,
,
则![]() ,
,
设![]() ,设上式为
,设上式为![]() ,
,
即有![]() ,
,
![]() ,即为
,即为![]() ,
,
解得![]() ,
,
则![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,AC=1,AB=![]() ,BC=
,BC=![]() ,AA1=
,AA1=![]() .
.

(1)求证:A1B⊥B1C;
(2)求二面角A1—B1C—B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若0<a<b,且a+b=1,则下列各式中最大的是( )
A.﹣1
B.log2a+log2b+1
C.log2b
D.log2(a3+a2b+ab2+b3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生期末考试数学成绩和总分年级排名如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学 | 115 | 112 | 93 | 125 | 145 |
年级排名 | 250 | 300 | 450 | 70 | 10 |
(1)通过大量事实证明发现,一个学生的数学成绩和总分年级排名具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示年级排名,求
表示年级排名,求![]() 与
与![]() 的回归方程;(其中
的回归方程;(其中![]() 都取整数)
都取整数)
(2)若在本次考试中,预计数学分数为120分的学生年级排名大概是多少?
参考数据和公式:![]() ,其中
,其中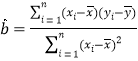 ,
,![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1+x﹣ ![]() +…+
+…+ ![]() ,g(x)=1﹣x+
,g(x)=1﹣x+ ![]() ﹣…﹣
﹣…﹣ ![]() ,设函数F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
,设函数F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
A.9
B.10
C.11
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|. (Ⅰ)若不等式f(x)≤2的解集为[0,4],求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若x0∈R,使得f(x0)+f(x0+5)﹣m2<4m,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com