
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率等于
的焦点,离心率等于![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求证
,求证![]() 为定值.
为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)分析题意可得b=1,再根据离心率的表达式和a,b,c之间的系数关系可求得标准方程
(2)将直线与椭圆方程进行联立,利用韦达定理,再结合题意即可
(1)设椭圆的标准方程为为![]() ,
,
由题b=1,![]() .即
.即![]() ,
,
∴椭圆C的方程为![]() .
.
(2)方法一:设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),M(0,y0).易知F点的坐标为(2,0).![]() ,
,
∴(x1,y1-y0)=λ1(2-x1,-y1),![]() ,
,
将A点坐代入到椭圆方程中,得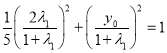 ,
,
去分母整理得![]() .同理,由
.同理,由![]() ,
,
可得![]() ,∴λ1,λ2是方程
,∴λ1,λ2是方程![]() 的两个根,∴λ1+λ2=-10.故λ1+λ2为定值.
的两个根,∴λ1+λ2=-10.故λ1+λ2为定值.
方法二:设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),M(0,y0).又易知F点的坐标为(2,0).显然直线![]() 存在斜率,设直线
存在斜率,设直线![]() 的斜率为k,则直线
的斜率为k,则直线![]() 的方程是y=k(x-2).将直线
的方程是y=k(x-2).将直线![]() 的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0.
的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0. ![]() .
.
又![]() ,将各点坐标代入得
,将各点坐标代入得
![]() ,
,
 ,
,
故λ1+λ2为定值.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.函数 在区间
在区间![]() 上有且只有
上有且只有![]() 个零点
个零点
B.若函数![]() ,则
,则![]()
C.如果函数![]() 在
在![]() 上单调递增,那么它在
上单调递增,那么它在![]() 上单调递减
上单调递减
D.若函数![]() 的图象关于点
的图象关于点![]() 对称,则函数
对称,则函数![]() 为奇函数
为奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,如图.
,如图.
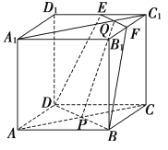
(1)若![]() 交平面
交平面![]() 于点
于点![]() ,证明:
,证明:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在确定
,若存在确定![]() 的位置,若不存在说明理由.
的位置,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
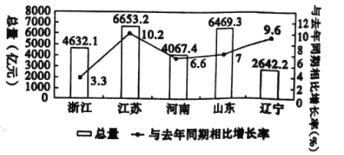
A. 2017年第一季度GDP增速由高到低排位第5的是浙江省.
B. 与去年同期相比,2017年第一季度的GDP总量实现了增长.
C. 去年同期河南省的GDP总量不超过4000亿元 .
D. 2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() 且
且![]() ,在数列
,在数列![]() 中,首项
中,首项![]() ,
,![]() 是其前
是其前![]() 项和,且
项和,且![]() ,
,![]() .
.
(1)设![]() ,
,![]() ,证明数列
,证明数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,证明数列
,证明数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(3)若当且仅当![]() 时,数列
时,数列![]() 取到最小值,求
取到最小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
(ii)在(i)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com