
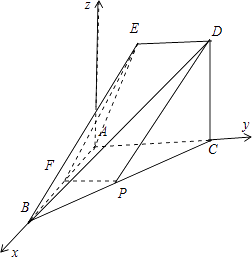
【题目】如图,已知ACDE是直角梯形,且ED∥AC,平面ACDE⊥平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2, ![]() ,P是BC的中点. (Ⅰ)求证:DP∥平面EAB;
,P是BC的中点. (Ⅰ)求证:DP∥平面EAB;
(Ⅱ)求平面EBD与平面ABC所成锐二面角大小的余弦值.
【答案】(I)证明:取AB的中点F,连接PF,EF. 又∵P是BC的中点,∴ ![]() .
.
∵ ![]() ,ED∥AC,
,ED∥AC,
∴ ![]() ,
,
∴四边形EFPD是平行四边形,
∴PD∥EF.
而EF平面EAB,PD平面EAB,
∴PD∥平面EAB.
(II)∵∠BAC=90°,平面ACDE⊥平面ABC,∴BA⊥平面ACDE.
以点A为坐标原点,直线AB为x轴,AC为y轴,建立如图所示的空间直角坐标系,
则z轴在平面EACD内.则A(0,0,),B(2,0,0), ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() .
.
设平面EBD的法向量 ![]() ,由
,由 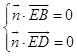 ,得
,得  ,
,
取z=2,则 ![]() ,y=0.∴
,y=0.∴ ![]() .
.
可取 ![]() 作为平面ABC的一个法向量,
作为平面ABC的一个法向量,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
即平面EBD与平面ABC所成锐二面角大小的余弦值为 ![]() .
.
【解析】(I)取AB的中点F,连接PF,EF.利用三角形的中位线定理可得 ![]() .再利用已知条件和平行四边形的判定定理可得四边形EFPD是平行四边形,可得PD∥EF.利用线面平行的判定定理即可得出;(II)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
.再利用已知条件和平行四边形的判定定理可得四边形EFPD是平行四边形,可得PD∥EF.利用线面平行的判定定理即可得出;(II)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,AB⊥平面BCD,CD⊥BD. 
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A﹣MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +y2=1. (Ⅰ)求椭圆C的长轴和短轴的长,离心率e,左焦点F1;
+y2=1. (Ⅰ)求椭圆C的长轴和短轴的长,离心率e,左焦点F1;
(Ⅱ)经过椭圆C的左焦点F1作直线l,直线l与椭圆C相交于A,B两点,若|AB|= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() +
+ ![]() =1表示焦点在y轴上的椭圆,命题q:双曲线
=1表示焦点在y轴上的椭圆,命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() ),若命题p、q中有且只有一个为真命题,则实数m的取值范围是
),若命题p、q中有且只有一个为真命题,则实数m的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列4个命题: ①“若x+y=0,则x,y互为相反数”的逆否命题;
②“若a>b,则a2>b2”的逆命题;
③“若x≤﹣3,则x2﹣x﹣6>0”的否命题;
④“若ab是无理数,则a,b是无理数”的逆命题.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且在(﹣∞,0]上是增函数,设 ![]() ,c=f(0.20.6),则a,b,c的大小关系是( )
,c=f(0.20.6),则a,b,c的大小关系是( )
A.c<b<a
B.b<c<a
C.b<a<c
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆具有性质:若M,N是椭圆C: ![]() =1(a>b>0且a,b为常数)上关于y轴对称的两点,P是椭圆上的左顶点,且直线PM,PN的斜率都存在(记为kPM , kPN),则kPMkPN=
=1(a>b>0且a,b为常数)上关于y轴对称的两点,P是椭圆上的左顶点,且直线PM,PN的斜率都存在(记为kPM , kPN),则kPMkPN= ![]() .类比上述性质,可以得到双曲线的一个性质,并根据这个性质得:若M,N是双曲线C:
.类比上述性质,可以得到双曲线的一个性质,并根据这个性质得:若M,N是双曲线C: ![]() =1(a>0,b>0)上关于y轴对称的两点,P是双曲线C的左顶点,直线PM,PN的斜率都存在(记为kPM , kPN),双曲线的离心率e=
=1(a>0,b>0)上关于y轴对称的两点,P是双曲线C的左顶点,直线PM,PN的斜率都存在(记为kPM , kPN),双曲线的离心率e= ![]() ,则kPMkPN等于 .
,则kPMkPN等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com