
【题目】如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1 , CC1的中点,且BE⊥B1F. 
(Ⅰ)求证:B1F⊥EC1;
(Ⅱ)求二面角C1﹣BE﹣C的余弦值.
【答案】证明:(Ⅰ)分别取BC1 , BC中点D,G,连结ED,AG, ∵ABC﹣A1B1C1是直三棱柱,且底面是正三角形,
∴AG⊥面BCC1B1 ,
又∵E,D都是中点,∴ED∥AG,则ED⊥面BCC1B1 , 可得ED⊥B1F,
已知BE⊥B1F,且BE∩ED=E,∴B1F⊥面BEC1 , 则B1F⊥EC1;
(Ⅱ)解:由(Ⅰ)知B1F⊥面BEC1 , ∴B1F⊥BC1 , 则△B1C1F∽△BB1C1 ,
∴ ![]() ,设BB1=a,则C1F=
,设BB1=a,则C1F= ![]() ,代入得a=
,代入得a= ![]() ,
,
以O为原点,OE为x轴,OC为y轴,过O作平面ABC的垂线为z轴,建立如图坐标系O﹣xyz,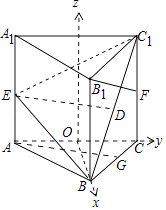
得C(0,2,0),B( ![]() ,0,0),E(0,﹣2,
,0,0),E(0,﹣2, ![]() ),
),
C1(0,2,4 ![]() ),B1(
),B1( ![]() ,0,
,0, ![]() ),F(0,2,2
),F(0,2,2 ![]() ).
).
∵B1F⊥面BEC1 , ∴平面BEC1的一个法向量为 ![]() ;
;
设平面BEC的一个法向量为 ![]() ,
,
则 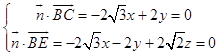 ,取x=
,取x= ![]() ,得y=3,z=
,得y=3,z= ![]() .
.
∴ ![]() .
.
∴cos< ![]() >=
>=  =
= ![]() =-
=- ![]() .
.
∴二面角C1﹣BE﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)分别取BC1 , BC中点D,G,连结ED,AG,推导出AG⊥面BCC1B1 , 从而ED⊥B1F,BE⊥B1F,由此能证明B1F⊥面BEC1 , 进一步得到B1F⊥EC1;(Ⅱ)以O为原点,OE为x轴,OC为y轴,过O作平面ABC的垂线为z轴,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角C1﹣BE﹣C的余弦值.


科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣2)2+(y﹣1)2=1,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA,PB,其中A,B为切点,则 ![]() 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC= ![]() ,BC⊥BE,∠ABE=
,BC⊥BE,∠ABE= ![]() .
.
(1)求证:BC⊥平面ABEF;
(2)求平面ACF与平面BCE所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P在双曲线 ![]() (a>0,b>0)的右支上,其左、右焦点分别为F1、F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为( )
(a>0,b>0)的右支上,其左、右焦点分别为F1、F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为( )
A.± ![]()
B.± ![]()
C.± ![]()
D.± ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,截至2016年底全国微信注册用户数量已经突破9.27亿,为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量(个) | 频数 | 频率 |
0~4 | 0.15 | |
5~8 | 40 | 0.4 |
9~12 | 25 | |
13~16 | a | c |
16以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值及样本中微信群个数超过12的概率;
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D=  ,给出下列四个命题:
,给出下列四个命题:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcosB,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsinC,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)Sn为数列{an}的前n项和.已知an>0,an2+2an=4Sn+3,
(1)求{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com