
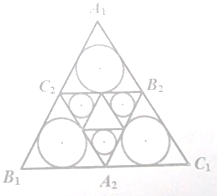
 ÉèÕýÈý½ÇÐÎA1B1C1±ß³¤Îªa£¬·Ö±ðÈ¡B1C1£¬C1A1£¬A1B1µÄÖеãA2£¬B2£¬C2£¬¼Ça1ÊÇÕýÈý½ÇÐÎA1B1C1³ýÈ¥¡÷A2B2C2ºóʣϵÄÈý¸öÄÚÇÐÔ²Ãæ»ýÖ®ºÍ£¬ÒÀ´ËÀàÍÆ£º¼ÇanÊÇ¡÷AnBnCn³ýÈ¥¡÷An+1Bn+1Cn+1ºóʣϵÄÈý¸öÈý½ÇÐÎÄÚÇÐÔ²Ãæ»ýÖ®ºÍ£¬´Ó¶øµÃµ½ÊýÁÐ{an}£¬ÉèÕâ¸öÊýÁÐ{an}µÄÇ°nÏîºÍSn£®
ÉèÕýÈý½ÇÐÎA1B1C1±ß³¤Îªa£¬·Ö±ðÈ¡B1C1£¬C1A1£¬A1B1µÄÖеãA2£¬B2£¬C2£¬¼Ça1ÊÇÕýÈý½ÇÐÎA1B1C1³ýÈ¥¡÷A2B2C2ºóʣϵÄÈý¸öÄÚÇÐÔ²Ãæ»ýÖ®ºÍ£¬ÒÀ´ËÀàÍÆ£º¼ÇanÊÇ¡÷AnBnCn³ýÈ¥¡÷An+1Bn+1Cn+1ºóʣϵÄÈý¸öÈý½ÇÐÎÄÚÇÐÔ²Ãæ»ýÖ®ºÍ£¬´Ó¶øµÃµ½ÊýÁÐ{an}£¬ÉèÕâ¸öÊýÁÐ{an}µÄÇ°nÏîºÍSn£®| ¦Ð¦Á2 |
| 12 |
| 1 |
| 3 |
(
|
| 1 |
| 3 |
| ||
| 12 |
| ||
| 12 |
| 9¦Ða2 |
| 144 |
| 9¦Ða2 |
| 144 |
| 1 |
| 4 |
| 9¦Ða2 |
| 144 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| ¦Ð¦Á2 |
| 12 |
| 1 |
| 2 |
| 1 |
| 3 |
(
|
| 1 |
| 3 |
| ||
| 12 |
| ||
| 12 |
| 9¦Ða2 |
| 144 |
| 9¦Ða2 |
| 144 |
| 1 |
| 4 |
| 9¦Ða2 |
| 144 |
| 1 |
| 4 |
| 9¦Ða2 |
| 144 |
| 1 |
| 4 |
| 9¦Ða2 |
| 144 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9¦Ða2 |
| 144 |
1-(
| ||
1-
|
| ¦Ða2 |
| 12 |
| 1 |
| 4n |
| 1 |
| 4n |
| ¦Ð¦Á2 |
| 12 |



| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
A¡¢£¨
| ||
B¡¢£¨0£¬
| ||
| C¡¢£¨1£¬3£© | ||
D¡¢£¨1£¬
|
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
| 1 |
| 2 |
A¡¢
| ||
B¡¢
| ||
C¡¢
| ||
D¡¢
|
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
| ¦Ð |
| 2 |
| x | x1 |
| x2 |
| x3 | ||||
| ¦Øx+ϕ | 0 |
| ¦Ð |
| 2¦Ð | ||||
| f£¨x£© | y1 | 3 | y2 | -1 | y3 |
| C |
| 2 |
| A |
| 2 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
 ÒÑÖª{an}Êǹ«²î²»Îª0µÄµÈ²îÊýÁУ¬a1=3£¬ÏÖ½«ÊýÁÐ{an}µÄ¸÷ÏîÒÀ´Î·ÅÈëÈçͼ±í¸ñÖУ¬ÆäÖеÚ1ÐÐ1ÏµÚ2ÐÐ2Ï¡£¬µÚnÐÐ2n-1Ï¼ÇµÚnÐи÷ÏîµÄºÍΪTn£¬ÇÒT1£¬T2£¬T3³ÉµÈ±ÈÊýÁУ®ÊýÁÐ{an}µÄͨÏʽÊÇ£¨¡¡¡¡£©
ÒÑÖª{an}Êǹ«²î²»Îª0µÄµÈ²îÊýÁУ¬a1=3£¬ÏÖ½«ÊýÁÐ{an}µÄ¸÷ÏîÒÀ´Î·ÅÈëÈçͼ±í¸ñÖУ¬ÆäÖеÚ1ÐÐ1ÏµÚ2ÐÐ2Ï¡£¬µÚnÐÐ2n-1Ï¼ÇµÚnÐи÷ÏîµÄºÍΪTn£¬ÇÒT1£¬T2£¬T3³ÉµÈ±ÈÊýÁУ®ÊýÁÐ{an}µÄͨÏʽÊÇ£¨¡¡¡¡£©| A¡¢an=2n+1 |
| B¡¢an=3n |
| C¡¢an=4n-1 |
| D¡¢an=2n-1 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
| AM |
| MB |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
| 1 |
| log2an•log2an+1 |
| 2 |
| 3 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
| x2 |
| 2 |
| 13 |
| 20 |
²é¿´´ð°¸ºÍ½âÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com