
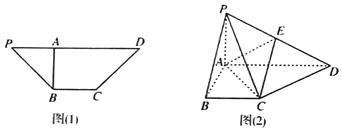
【题目】如图![]() 在四边形PBCD中,
在四边形PBCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图
,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图![]() 所示图形.
所示图形.
![]() Ⅰ
Ⅰ![]() 求证:平面
求证:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若点E是PD的中点,求三棱锥
若点E是PD的中点,求三棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,若数列
,若数列![]() 满足:对所有
满足:对所有![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() ,则称
,则称![]() 为“
为“![]() 数列”,设
数列”,设![]() R,函数
R,函数 ,数列
,数列![]() 满足
满足![]() ,
,![]() (
(![]() ).
).
(1)若![]() ,而
,而![]() 是
是![]() 数列,求
数列,求![]() 的值;
的值;
(2)设![]() ,证明:存在
,证明:存在![]() ,使得
,使得![]() 是
是![]() 数列,但对任意
数列,但对任意![]() ,
,![]() 都不是
都不是![]() 数列;
数列;
(3)设![]() ,证明:对任意
,证明:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 是
是![]() 数列.
数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上,给定非零向量![]() ,对任意向量
,对任意向量![]() ,定义
,定义![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,证明:若位置向量
,证明:若位置向量![]() 的终点在直线
的终点在直线![]() 上,则位置向量
上,则位置向量![]() 的终点也在一条直线上;
的终点也在一条直线上;
(3)已知存在单位向量![]() ,当位置向量
,当位置向量![]() 的终点在抛物线
的终点在抛物线![]() :
:![]() 上时,位置向量
上时,位置向量![]() 终点总在抛物线
终点总在抛物线![]() :
:![]() 上,曲线
上,曲线![]() 和
和![]() 关于直线
关于直线![]() 对称,问直线
对称,问直线![]() 与向量
与向量![]() 满足什么关系?
满足什么关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为![]() 为参数
为参数![]() 以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为
以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为![]() ,且圆心C在直线l上.
,且圆心C在直线l上.
![]() Ⅰ
Ⅰ![]() 求直线l的直角坐标方程及圆C的极坐标方程;
求直线l的直角坐标方程及圆C的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 是直线l上一点,
是直线l上一点,![]() 是圆C上一点,求
是圆C上一点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子科技公司由于产品采用最新技术,销售额不断增长,最近![]() 个季度的销售额数据统计如下表(其中
个季度的销售额数据统计如下表(其中![]() 表示
表示![]() 年第一季度,以此类推):
年第一季度,以此类推):
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y(百万元) |
|
|
|
|
|
(1)公司市场部从中任选![]() 个季度的数据进行对比分析,求这
个季度的数据进行对比分析,求这![]() 个季度的销售额都超过
个季度的销售额都超过![]() 千万元的概率;
千万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 的销售额.
的销售额.
附:线性回归方程:![]() 其中
其中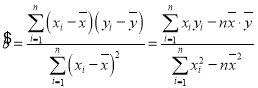 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过
经过![]() ,
, ![]() 两点,且圆心在直线
两点,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 内一点
内一点![]() 作两条相互垂直的弦
作两条相互垂直的弦![]() ,当
,当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
(3)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点, ![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com