Question

【题目】如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题： ①平面A′FG⊥平面ABC；
②BC∥平面A′DE；
③三棱锥A′﹣DEF的体积最大值为 a3；
④动点A′在平面ABC上的射影在线段AF上；
⑤二面角A′﹣DE﹣F大小的范围是[0， ]．
其中正确的命题是（写出所有正确命题的编号）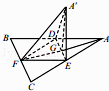

Answer 1

【答案】①②③④
【解析】解：①由已知可得四边形ADEF是菱形，则DE⊥GA′，DE⊥GF， ∴DE⊥平面A′FG，∴平面A′FG⊥平面ABC，①正确；
②由三角形中位线定理可得BC∥DE，∴BC∥平面A′DE，∴②正确；
③当面A′DE⊥面ABC时，三棱锥A′﹣DEF的体积达到最大，
最大值为 = ，③正确；
④由平面A′FG⊥平面ABC，可知点A′在面ABC上的射影在线段AF上，∴④正确；
⑤在旋转过程中二面角A′﹣DE﹣F大小的范围是[0，π]，∴⑤不正确．
所以答案是：①②③④．
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系，以及对直线与平面平行的判定的理解，了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．