
【题目】设圆 ![]() 的圆心为F1 , 直线l过点F2(2,0)且不与x轴、y轴垂直,且与圆F1于C,D两点,过F2作F1C的平行线交直线F1D于点E,
的圆心为F1 , 直线l过点F2(2,0)且不与x轴、y轴垂直,且与圆F1于C,D两点,过F2作F1C的平行线交直线F1D于点E,
(1)证明||EF1|﹣|EF2||为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线Γ,直线l交Γ于M,N两点,过F2且与l垂直的直线与圆F1交于P,Q两点,求△PQM与△PQN的面积之和的取值范围.
【答案】
(1)证明:圆 ![]() ,圆心F1(﹣2,0),半径r=2,如图所示.
,圆心F1(﹣2,0),半径r=2,如图所示.
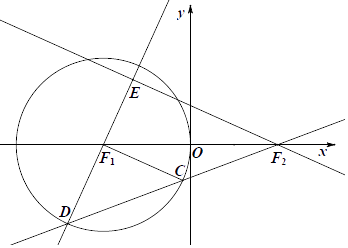
因为F1C∥EF2,所以∠F1CD=∠EF2D.
又因为F1D=F1C,所以∠F1CD=∠F1DC,
所以∠EF2D=∠F1DC,
又因为∠F1DC=∠EDF2,所以∠EF2D=∠EDF2,
故ED=EF2,可得||EF1|﹣|EF2||=||EF1|﹣|ED||=|F1D|=2<|F1F2|,
根据双曲线的定义,可知点E的轨迹是以F1,F2为焦点的双曲线(顶点除外),
且a=1,c=2,b= ![]() =
= ![]() ,
,
故点E的轨迹方程为 ![]()
(2)解: ![]() .
.
依题意可设l:x=my+2(m≠0),M(x1,y1),N(x2,y2),
由于PQ⊥l,设lPQ:y=﹣m(x﹣2).
圆心F1(﹣2,0)到直线PQ的距离 ![]() ,
,
所以 ![]() ,
,
又因为d<2,解得 ![]() .
.
联立直线l与双曲线Γ的方程 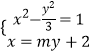 ,消去x得(3m2﹣1)y2+12my+9=0,
,消去x得(3m2﹣1)y2+12my+9=0,
则 ![]() ,
,
所以 ![]() ,
,
记△PQM,△PQN的面积分别为S1,S2,
则 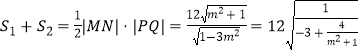 ,
,
又因为 ![]() ,所以S1+S2∈(12,+∞),
,所以S1+S2∈(12,+∞),
所以S1+S2的取值范围为(12,+∞)
【解析】(1)求得圆F1的圆心和半径,运用平行线的性质和等腰三角形的性质,可得ED=EF2,再由双曲线的定义,即可得到所求定值和双曲线的方程;(2)设出l:x=my+2(m≠0),lPQ:y=﹣m(x﹣2),设M(x1,y1),N(x2,y2),求出圆心到直线PQ的距离,运用弦长公式可得|PQ|;再由直线l的方程和双曲线的方程联立,运用韦达定理和弦长公式,可得|MN|,再由三角形的面积公式可得△PQM与△PQN的面积之和为 ![]() |MN||PQ|,化简整理,结合不等式的性质,即可得到所求范围.
|MN||PQ|,化简整理,结合不等式的性质,即可得到所求范围.


科目:高中数学 来源: 题型:
【题目】如图,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( ) 
A.当|CD|=2|AB|时,M,N两点不可能重合
B.M,N两点可能重合,但此时直线AC与直线l不可能相交
C.当AB与CD相交,直线AC平行于l时,直线BD可以与l相交
D.当AB,CD是异面直线时,MN可能与l平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资. (Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
雕刻量n | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列{an}满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn , 每段螺旋线与其所在的正方形所围成的扇形面积为cn , 则下列结论错误的是( )
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn , 每段螺旋线与其所在的正方形所围成的扇形面积为cn , 则下列结论错误的是( ) 
A.![]()
B.a1+a2+a3+…+an=an+2﹣1
C.a1+a3+a5+…+a2n﹣1=a2n﹣1
D.4(cn﹣cn﹣1)=πan﹣2an+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N. 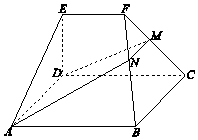
(Ⅰ)求证:AD∥MN;
(Ⅱ)求证:平面ADMN⊥平面CDEF;
(Ⅲ)若CD⊥EA,EF=ED,CD=2EF,平面ADE∩平面BCF=l,求二面角A﹣l﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是直角梯形,侧棱SA丄底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点.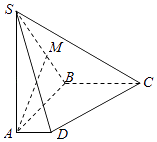
(1)求证:AM∥平面SCD;
(2)求平面SCD与平面SAB所成的二面角的余弦值;
(3)设点N是直线CD上的动点,MN与平面SAB所成的角为θ,求sinθ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心),两圆盘上分别有互相垂直的两条直径将其分为四个区域,小圆盘上所写的实数分别记为x1 , x2 , x3 , x4 , 大圆盘上所写的实数分别记为y1 , y2 , y3 , y4 , 如图所示.将小圆盘逆时针旋转i(i=1,2,3,4)次,每次转动90° , 记Ti(i=1,2,3,4)为转动i次后各区域内两数乘积之和,例如T1=x1y2+x2y3+x3y4+x4y1 . 若x1+x2+x3+x4<0,y1+y2+y3+y4<0,则以下结论正确的是( ) 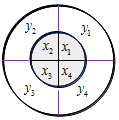
A.T1 , T2 , T3 , T4中至少有一个为正数
B.T1 , T2 , T3 , T4中至少有一个为负数
C.T1 , T2 , T3 , T4中至多有一个为正数
D.T1 , T2 , T3 , T4中至多有一个为负数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com