
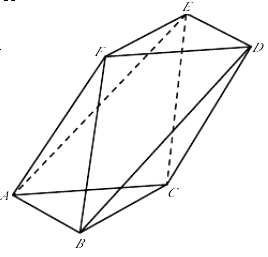
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2 ![]() .
. 
(1)求证:平面ABC⊥平面ACDF;
(2)求平面AEF与平面ACE所成的锐二面角的余弦值.
【答案】
(1)证明:设O是AC中点,连结OF、OB、FC,
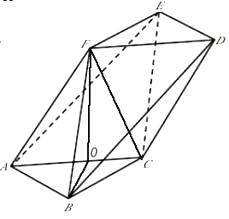
在△ABC中,AB=BC,∴OB⊥AC,
∵四边形ACDF是菱形,∠FAC=60°,
∴△FAC是等边三角形,∴OF⊥AC,
∴∠FOB是二面角F﹣AC﹣B的平面角,
在Rt△FAO中,AF=2 ![]() ,AO=
,AO= ![]() AC=
AC= ![]() AF=
AF= ![]() ,
,
∴OF= ![]() =
= ![]() ,
,
又∵BF= ![]() ,∴OF2+OB2=BF2,
,∴OF2+OB2=BF2,
∴∠FOB=90°,
∴平面ABC⊥平面ACDF.
(2)解:由(1)知OB、OC、OF两两垂直,以O为原点,OB为x轴,OC为y轴,OF为z轴,
建立空间直角坐标系,
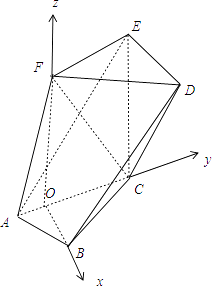
则A(0,﹣ ![]() ,0),B(
,0),B( ![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),F(0,0,3),
,0),F(0,0,3),
![]() =(0,
=(0, ![]() ,3),
,3), ![]() =(0,2
=(0,2 ![]() ,0),
,0),
∵AB∥DE,AF∥CD,又AB平面CDE,AF平面CDE,
DE平面CDE,CD平面CDE,
∴AB∥平面CDE,AF∥平面CDE,
又AB∩AF=A,∴平面ABF∥平面CDE,
∵EF∥BC,∴B、C、E、F四点共面,
又平面ABF∩平面BCEF=BF,平面CDE∩平面BCEF=CE,
∴BF∥CE,∴四边形BCEF是平行四边形,
∴ ![]() =
= ![]() =(﹣
=(﹣ ![]() ,0),
,0),
∴ ![]() =(﹣
=(﹣ ![]() ,3),
,3),
设平面AEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则 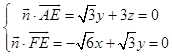 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
设平面ACE的法向量 ![]() =(a,b,c),
=(a,b,c),
则 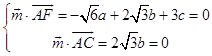 ,取a=
,取a= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
设平面AEF与平面ACE所成的锐二面角为θ,
则cosθ= ![]() =
= ![]() .
.
∴平面AEF与平面ACE所成的锐二面角的余弦值为 ![]() .
.
【解析】(1)设O是AC中点,连结OF、OB、FC,推导出OB⊥AC,OF⊥AC,则∠FOB是二面角F﹣AC﹣B的平面角,由此能证明平面ABC⊥平面ACDF.(2)以O为原点,OB为x轴,OC为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出平面AEF与平面ACE所成的锐二面角的余弦值.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
+lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不为0的等差数列{an}前n项和为Sn , 满足S4=2a5 , a1a2=a4 , 数列{bn}满足bn+1=2bn , b1=2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,c>0,函数f(x)=|x+a|﹣|x﹣b|+c的最大值为10.
(1)求a+b+c的值;
(2)求 ![]() (a﹣1)2+(b﹣2)2+(c﹣3)2的最小值,并求出此时a、b、c的值.
(a﹣1)2+(b﹣2)2+(c﹣3)2的最小值,并求出此时a、b、c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1,g(x)=lnx﹣ax+a,若存在x0∈(1,2),使得f(x0)g(x0)<0,则实数a的取值范围是( )
A.![]()
B.(ln2,e﹣1)
C.[1,e﹣1)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+ ![]() 中“”即代表无数次重复,但原式却是个定值,它可以通过方程1+
中“”即代表无数次重复,但原式却是个定值,它可以通过方程1+ ![]() =x求得x=
=x求得x= ![]() .类比上述过程,则
.类比上述过程,则 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx﹣xcosx(x≥0).
(1)求函数f(x)的图象在 ![]() 处的切线方程;
处的切线方程;
(2)若任意x∈[0,+∞),不等式f(x)<ax3恒成立,求实数a的取值范围;
(3)设m=![]() f(x)dx,
f(x)dx, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 分成左右两部分,在PQ 左侧部分三角形POQ 为观赏区,在PQ 右侧部分种草,已知种花的单位面积的造价为3a,种草的单位面积的造价为2a,其中a 为正常数,设∠AOP=θ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,设总造价为f(θ) 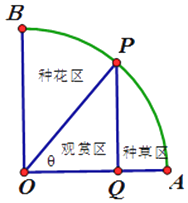
(1)求f(θ)关于θ 的函数关系式;
(2)求当θ 为何值时,总造价最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设 ![]() (α,β∈R),则α+β的取值范围是 .
(α,β∈R),则α+β的取值范围是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com