
 )n<3.
)n<3. )n=cn0+Cn1•
)n=cn0+Cn1• +Cn2•
+Cn2•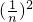 +…+Cnn•(
+…+Cnn•( )n>cn0+Cn1•
)n>cn0+Cn1• =2 (1分)
=2 (1分) +Cn2•
+Cn2•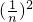 +…+Cnn•(
+…+Cnn•( )n
)n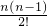 •
• +…+
+…+ •
•
 +…+
+…+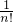 (2分)
(2分) +…+
+…+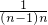
 )+…+(
)+…+( -
- )
) <3 (2分)
<3 (2分) )n=cn0+Cn1•
)n=cn0+Cn1• +Cn2•
+Cn2•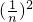 +…+Cnn•(
+…+Cnn•( )n只用前两项即可证明不等式的前半部分;再通过组合数的性质对等式右边进行放缩即可证明右边.
)n只用前两项即可证明不等式的前半部分;再通过组合数的性质对等式右边进行放缩即可证明右边.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:江苏二模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年江苏省苏锡常镇四市高考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com