
【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0)
,0)
D.(﹣∞,﹣ ![]() ]
]
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为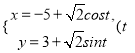 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 两点的极坐标和
两点的极坐标和![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问5分,(2)小问7分)
如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 过
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]()

(1)若![]() ,求椭圆的标准方程
,求椭圆的标准方程
(2)若![]() 求椭圆的离心率
求椭圆的离心率![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形ABCD中,AB=CD且异面直线AB与CD所成的角为30°,E,F为BC和AD的中点,则异面直线EF和AB所成的角为( )
A.15°
B.30°
C.45°或75°
D.15°或75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为 ![]() ,当
,当 ![]() 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意的x1∈[﹣1,2],存在x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.![]()
B.![]()
C.[3,+∞)
D.(0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养正中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),校总务处计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设![]() (单位:弧度),用
(单位:弧度),用![]() 表示弓形BCD的面积
表示弓形BCD的面积![]()
(2)如果该校总务处邀请你规划这块土地。如何设计![]() 的大小才能使总利润最大?并求出该最大值
的大小才能使总利润最大?并求出该最大值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com