已知函数
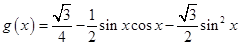
,将其图象向左移
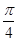
个单位,并向上移
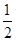
个单位,得到函数
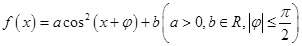
的图象.
(1)求实数
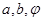
的值;
(2)设函数
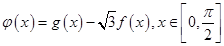
,求函数
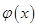
的单调递增区间和最值.
(1)
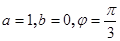
;(2)
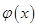
的单调增区间为
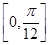
,最小值为
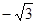
,最大值为
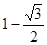
.
试题分析:(1) 利用倍角公式将
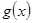
化简,然后平移化成
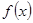
的形式,待定系数可得
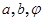
的值;(2)先求出
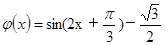
,当
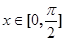
时,由
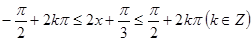
,得
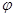
(x)的单调增区间为
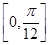
,最小值为
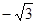
,最大值为
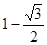
.
试题解析:(1)依题意化简得
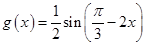
,平移g(x)得
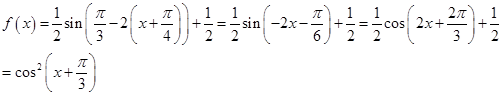
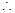
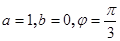
(2)
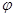
(x)=g(x)-
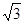
f(x)=
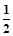
sin(2x+
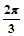
)-
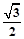
cos(2x+
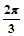
)-
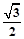
=sin(2x+
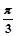
)-
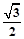
由
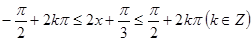
得
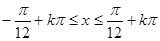
,因为
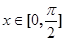
,所以当
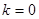
时,在
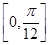
上单调增,∴
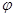
(x)的单调增区间为
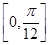
, 值域为
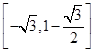
.,
故
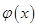
的最小值为
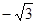
,最大值为
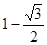
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
函数
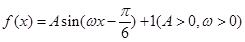
的最大值为3,其图像相邻两条对称轴之间的距离为
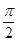
.
(1)求函数f(x)的解析式;
(2)设
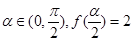
,求
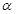
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
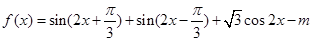
,若
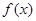
的最大值为1
(Ⅰ)求
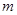
的值,并求
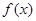
的单调递增区间;
(Ⅱ)在
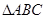
中,角
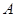
、
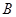
、
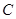
的对边
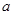
、
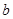
、
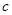
,若
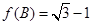
,且
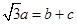
,试判断三角形的形状.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
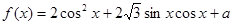
,且当
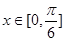
时,
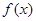
的最小值为2.
(1)求
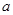
的值,并求
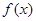
的单调增区间;
(2)将函数
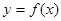
的图象上各点的纵坐标保持不变,横坐标缩短到原来的
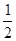
,再把所得图象向右平移
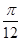
个单位,得到函数
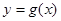
,求方程
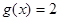
在区间
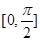
上的所有根之和.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
在△ABC中,角
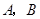
均为锐角,且
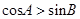
,则
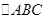
的形状是
三角形.
查看答案和解析>>

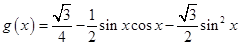 ,将其图象向左移
,将其图象向左移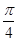 个单位,并向上移
个单位,并向上移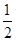 个单位,得到函数
个单位,得到函数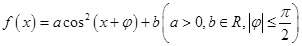 的图象.
的图象.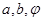 的值;
的值;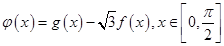 ,求函数
,求函数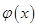 的单调递增区间和最值.
的单调递增区间和最值. 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案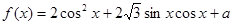 ,且当
,且当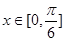 时,
时,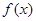 的最小值为2.
的最小值为2.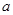 的值,并求
的值,并求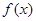 的单调增区间;
的单调增区间;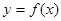 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的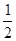 ,再把所得图象向右平移
,再把所得图象向右平移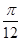 个单位,得到函数
个单位,得到函数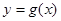 ,求方程
,求方程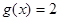 在区间
在区间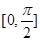 上的所有根之和.
上的所有根之和.