
 如图,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
如图,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?

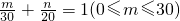 ,所以n=20(1-
,所以n=20(1-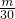 ),
), )=
)=
 =
=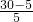 =
=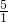


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
 如图,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
如图,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
查看答案和解析>>
科目:高中数学 来源:广东省湛师附中2010届高三第二次月考(理) 题型:解答题
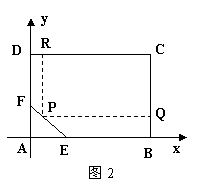 如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省江门市开平市风采华侨中学高一(下)第一次月考数学试卷(解析版) 题型:解答题
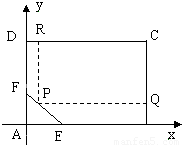
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com