
【题目】已知函数f(x)=2x+sinx,且f(y2﹣2y+3)+f(x2﹣4x+1)≤0,则当y≥1时, ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵f(x)=2x+sinx(x∈R),
∴f(﹣x)=﹣2x﹣sinx=﹣(2x+sinx)=﹣f(x),
即f(x)=2x+sinx(x∈R)是奇函数,
∵f(y2﹣2y+3)+f(x2﹣4x+1)≤0,
∴f(y2﹣2y+3)≤﹣f(x2﹣4x+1)=f[﹣(x2﹣4x+1)],
由f'(x)=1﹣cosx≥0,
∴函数单调递增.
∴(y2﹣2y+3)≤﹣(x2﹣4x+1),
即(y2﹣2y+3)+(x2﹣4x+1)≤0,
∴(y﹣1)2+(x﹣2)2≤1,
∵y≥1,
∴不等式对应的平面区域为圆心为(2,1),半径为1的圆的上半部分.![]() 的几何意义为动点P(x,y)到定点A(﹣1,0)的斜率的取值范围.
的几何意义为动点P(x,y)到定点A(﹣1,0)的斜率的取值范围.
设k= ![]() ,(k>0)
,(k>0)
则y=kx+k,即kx﹣y+k=0.
当直线和圆相切是,圆心到直线的距离d= ![]() =1,
=1,
即8k2﹣6k=0,解得k= ![]() .此时直线斜率最大.
.此时直线斜率最大.
当直线kx﹣y+k=0.经过点B(3,1)时,直线斜率最小,
此时3k﹣1+k=0,即4k=1,解得k= ![]()
∴ ![]() ≤k≤
≤k≤ ![]() ,
,
故选:A.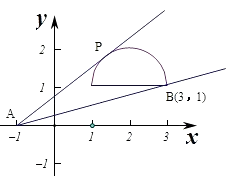
【考点精析】通过灵活运用奇偶性与单调性的综合,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx,其中常数a>0.
(Ⅰ)当a>2时,求函数f(x)的单调递增区间;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0 , h(x0))处的切线方程为l:y=g(x),若 ![]() >0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
(I)求证:AC⊥平面BCE;
(II)求三棱锥E﹣BCF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
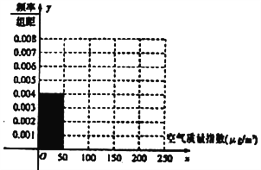
【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 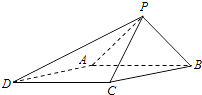
(1)求证:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】种植于道路两侧、为车辆和行人遮阴并构成街景的乔木称为行道树![]() 为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离
为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离![]() 按照北京市
按照北京市![]() 行道树修剪规范
行道树修剪规范![]() 要求,当树木与原有电力线发生矛盾时,应及时修剪树枝
要求,当树木与原有电力线发生矛盾时,应及时修剪树枝![]() 行道树修剪规范
行道树修剪规范![]() 中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表
中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表
电力线 | 安全距离 | |
水平距离 | 垂直距离 | |
|
|
|
|
|
|
|
|
|
|
|
|
330KV |
|
|
500KV |
|
|
现有某棵行道树已经自然生长2年,高度为![]() 据研究,这种行道树自然生长的时间
据研究,这种行道树自然生长的时间![]() 年
年![]() 与它的高度
与它的高度![]() 满足关系式
满足关系式![]()
![]() 1
1![]() ______;
______;![]() 将结果直接填写在答题卡的相应位置上
将结果直接填写在答题卡的相应位置上![]()
![]() 2
2![]() 如果这棵行道树的正上方有35kV的电力线,该电力线距地面
如果这棵行道树的正上方有35kV的电力线,该电力线距地面![]() 那么这棵行道树自然生长多少年必须修剪?
那么这棵行道树自然生长多少年必须修剪?
![]() 3
3![]() 假如这棵行道树的正上方有500KV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少米?
假如这棵行道树的正上方有500KV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).
(a∈R,e为自然对数的底数).
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)当a=1时,若直线l:y=kx-1与曲线y=f(x)相切,求l的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在原点,焦点在x轴上,椭圆的左顶点坐标为![]() ,离心率为
,离心率为![]() .
.
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 过点
过点![]() 作直线l交E于P、Q两点,试问:在x轴上是否存在一个定点M,使
作直线l交E于P、Q两点,试问:在x轴上是否存在一个定点M,使![]() 为定值?若存在,求出这个定点M的坐标;若不存在,请说明理由.
为定值?若存在,求出这个定点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com