(本题满分16分)
设数列
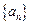
的前
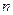
项和为
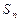
,若对任意
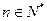
,都有
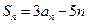
.
⑴求数列
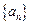
的首项;
⑵求证:数列
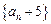
是等比数列,并求数列
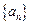
的通项公式;
⑶数列
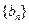
满足
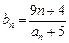
,问是否存在
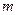
,使得
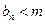
恒成立?如果存在,求出
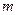
的值,如果不存在,说明理由.

,
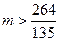
解:
⑴∵


∴

……………………………3分
⑵∵
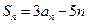
∴
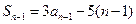
(
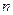
≥2)
∴
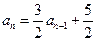
………………………………5分
∴


∴

(为常数) (
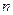
≥2)
∴数列
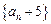
是以

为公比的等比数列 …………………………………7分
∴


…………………………………10分
⑶∵
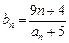
∴
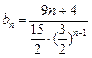
∴

………………………………12分
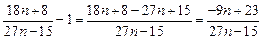
………………………………14分
∴当
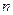
≥3时,

<1; 当
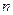
=2时,

>1
∴当

2时,
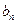
有最大值

∴

…………………………………15分
∴
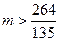

…………………………………16分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
正项数列
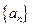
满足
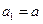
,
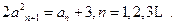
(1)若
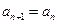
,求
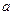
的值;
(2)当
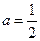
时,证明:
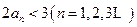
;
(3)设数列
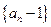
的前
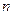
项之积为
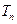
,若对任意正整数
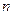
,总有
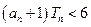
成立,求
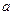
的取值范围
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(满分12分)
已知数列
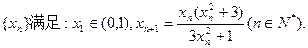
(1)证明:对任意的
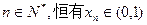
;
(2)对于
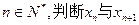
的大小关系,并证明你的结论。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题12分)
已知
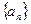
是等差数列,且
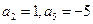
①求
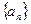
的通项
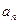
。
②求
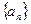
的前n项和S
n的最大值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
探索如下规律:
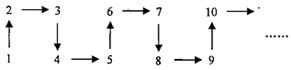
则根据规律,从2010、2011到2

012箭头的方向是 ( )
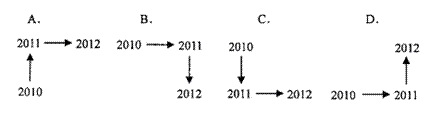
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
数列
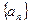
中,
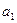
=15,
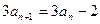
(
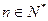
),则该数列中相邻两项的乘积是负数的是( )

查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
等比数列{
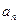
}的前n 项和为
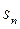
,已知
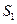
,
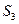
,
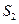
成等差数列
(1)求{
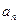
}的公比q
(2)若
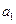
-
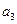
=3,求
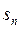
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列
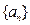
,
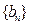
满足
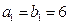
,
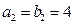
,
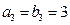
。
(1)若
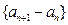
是等差数列,求
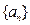
的通项公式;
(2)若
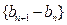
是等比数列,求
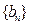
的通项公式;
(3)在(1)、(2)的条件下,当
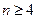
时,
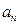
与
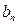
哪一个较大?证明你的结论。
查看答案和解析>>

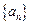 的前
的前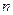 项和为
项和为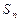 ,若对任意
,若对任意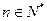 ,都有
,都有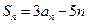 .
.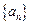 的首项;
的首项;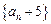 是等比数列,并求数列
是等比数列,并求数列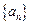 的通项公式;
的通项公式;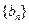 满足
满足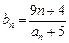 ,问是否存在
,问是否存在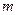 ,使得
,使得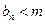 恒成立?如果存在,求出
恒成立?如果存在,求出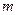 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.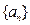 ,
,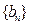 满足
满足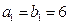 ,
,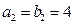 ,
,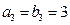 。
。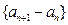 是等差数列,求
是等差数列,求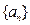 的通项公式;
的通项公式;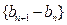 是等比数列,求
是等比数列,求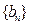 的通项公式;
的通项公式;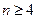 时,
时,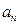 与
与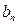 哪一个较大?证明你的结论。
哪一个较大?证明你的结论。