(本小题满分8分)
数列
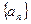
满足
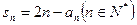
。
(Ⅰ)计算
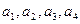
,并由此猜想通项公式
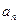
;
(Ⅱ)用数学归纳法证明(Ⅰ)中的猜想。
解:(Ⅰ)当

时,

,所以

。
当

时,

,所以

。
同理:

,

。
由此猜想

…………………………………………………5分
(Ⅱ)证明:①当

时,左边

,右边

,结论成立。
②假设

时,结论成立,即

,
那么

时,

,
所以

,所以

,
这表明

时,结论成立。
由①②知对一切

猜想

成立。 ……………………………8分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
已知等差数列

的前n项和为

,且满足

,则数列

的公差( )
A. | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知数列

满足

,且
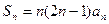
,
(1)求

的值;猜想
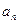
的表达式并用数学归纳法证明
(2)求

查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
已知数列

中,

(1)求数列

的通项公式;
(2)设

(3)设

是否存在最大的整数m,使得
对任意

,均有

成立?若存在,求出m,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分8分)
已知
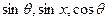
成等差数列,
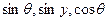
成等比数列。
证明:
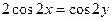
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)已知数列

是首项

公比

的等比数列,设

,数列

满足
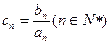
.
(1)求证:

是等差数列;
(2)求数列

的前n项和S
n;
(3)若

对一切正整数

恒成立,求实数
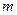
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)已知数列

满足

某同学欲求

的通项公式,他想,如能找到一个函数

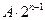



,把递推关系变成


后,就容易求出

的通项了.
(Ⅰ)请问:他设想的

存在吗?

的通项公式是什么?
(Ⅱ)记

,若不等式
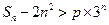
对任意

都成立,求实数

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(12分)已知数列
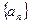
中,
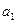
=2,
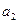
=3,其前
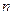
项和
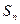
满足
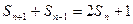
(
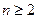
,
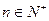
)。
(1)求证:数列
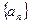
为等差数列,并求
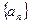
的通项公式;
(2)设
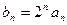
,求数列
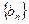
的前
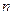
项和
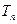
;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
(1)
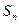
为等差数列{a
n}的前n项和,
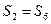
,
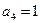
,求
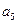
.
(2)在等比数列
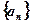
中,若
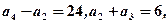
求首项
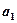
和公比
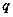
。
查看答案和解析>>

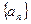 满足
满足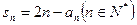 。
。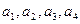 ,并由此猜想通项公式
,并由此猜想通项公式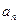 ;
; 中,
中,
 的通项公式;
的通项公式;
 是否存在最大的整数m,使得
是否存在最大的整数m,使得 ,均有
,均有 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。 是首项
是首项 公比
公比 的等比数列,设
的等比数列,设 ,数列
,数列 满足
满足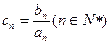 .
.  是等差数列;
是等差数列;  的前n项和Sn;
的前n项和Sn; 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 满足
满足
 的通项公式,他想,如能找到一个函数
的通项公式,他想,如能找到一个函数
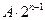


 ,把递推关系变成
,把递推关系变成
 后,就容易求出
后,就容易求出 的通项了.
的通项了. 存在吗?
存在吗? 的通项公式是什么?
的通项公式是什么? ,若不等式
,若不等式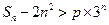 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.