
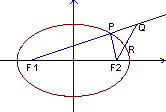
已知椭圆![]() =1,点P为其上一点,F1、F2为椭圆的焦点,Q为射线
=1,点P为其上一点,F1、F2为椭圆的焦点,Q为射线![]() 延长线上一点,且|PQ|=|PF2|,设R为F2Q的中点。
延长线上一点,且|PQ|=|PF2|,设R为F2Q的中点。
(1)当P点在椭圆上运动时,求R形成的轨迹方程;
(2)设点R形成的曲线为C,直线l:y=k(x+4![]() )与曲线C相交于A、B两点,若∠AOB=90o时,
)与曲线C相交于A、B两点,若∠AOB=90o时,
求k的值.
(请注意把答案填写在答题卡上)
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 20 |
| 1 |
| 4 |
| 1 |
| 25 |
| x2 |
| 2 |
| y2 |
| a |
| OR |
| OS |
查看答案和解析>>
科目:高中数学 来源:2012年云南省昆明市高三复习教学质量检测数学试卷(文科)(解析版) 题型:解答题
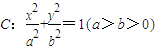 经过点P
经过点P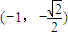 ,两焦点为F1、F2,短轴的一个端点为D,且
,两焦点为F1、F2,短轴的一个端点为D,且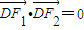 .
.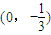 ,且交椭圆C于A、B两点,证明:以AB为直径的圆恒过定点T(0,1).
,且交椭圆C于A、B两点,证明:以AB为直径的圆恒过定点T(0,1).查看答案和解析>>
科目:高中数学 来源:2012年天津市高考数学试卷(文科)(解析版) 题型:解答题
 ,点P(
,点P( )在椭圆上.
)在椭圆上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com